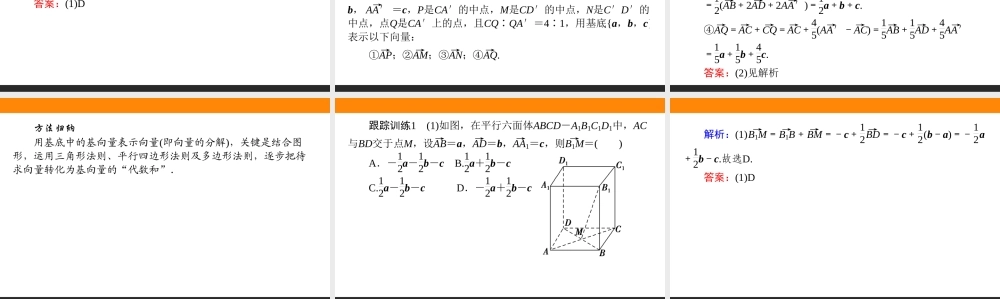
1.2空间向量基本定理最新课标1.了解空间向量基本定理及意义;2.掌握空间向量的线性运算;3.会用空间向量基本定理证明线线、线面关系.[教材要点]要点空间向量基本定理1.空间向量基本定理:如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得:p=________________.xa+yb+zc2.基底与基向量:如果三个向量a,b,c不共面,那么所有空间向量组成的集合就是{p|p=xa+yb+zc,x,y,z∈R},这个集合可看作由向量a,b,c生成的,我们把________________叫做空间的一个基底,a,b,c都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.{a,b,c}状元随笔(1)若p→=xa→+yb→+zc→,则xa→+yb→+zc→叫做向量a→,b→,c→的线性表达式或线性组合,或者说p→可以由a→,b→,c→线性表示.(2)对于基底{a→,b→,c→},除了应知道a→,b→,c→不共面外,还应明确以下三点:①基底选定后,空间的所有向量均可由基底唯一表示.选用不同的基底,同一向量的表达式也可能不同;②由于0与任意一个非零向量共线,与任意两个非零向量共面,所以若三个向量不共面,就说明它们都不是0;③空间的一个基底是指一个向量组,是由三个不共面的空间向量构成的;一个基向量是指基底中的某个向量,二者是相关联的不同概念.[教材答疑]教材P11探究证明:设向量a,b,c不共面(如图所示).过点O作OA→=a,OB→=b,OC→=c,OP→=p,过点P作直线PP′平行于OC,交平面OAB于点P′,在平面OAB内,过P′作直线P′A′∥OB,P′B′∥OA,分别与直线OA,OB相交于点A′,B′,于是存在三个实数x,y,z,使OA′→=xOA→=xa,OB′→=yOB→=yb,P′P→=zOC→=zc,OP→=OA′→+OB′→+P′P→=xOA→+yOB→+zOC→,即OP→=p=xa+yb+zc①.如果p=xa+yb+zc=x′a+y′b+z′c,那么可推出x=x′,y=y′,z=z′,这也证明了表达式①是唯一的.[基础自测]1.判断正误(正确的画“√”,错误的画“×”)(1)只有两两垂直的三个向量才能作为空间向量的一组基底.()(2)对于三个不共面向量a1,a2,a3,不存在实数组{λ1,λ2,λ3}使0=λ1a1+λ2a2+λ3a3.()(3)基底选定后,空间的所有向量均可由基底唯一表示.()(4)空间的一个基底是指一个向量组,是由三个不共面的空间向量构成的.()××√√2.已知{a,b,c}是空间的一个基底,则可以与向量p=a+b,q=a-b构成基底的向量是()A.aB.bC.a+2bD.a+2c解析:A...