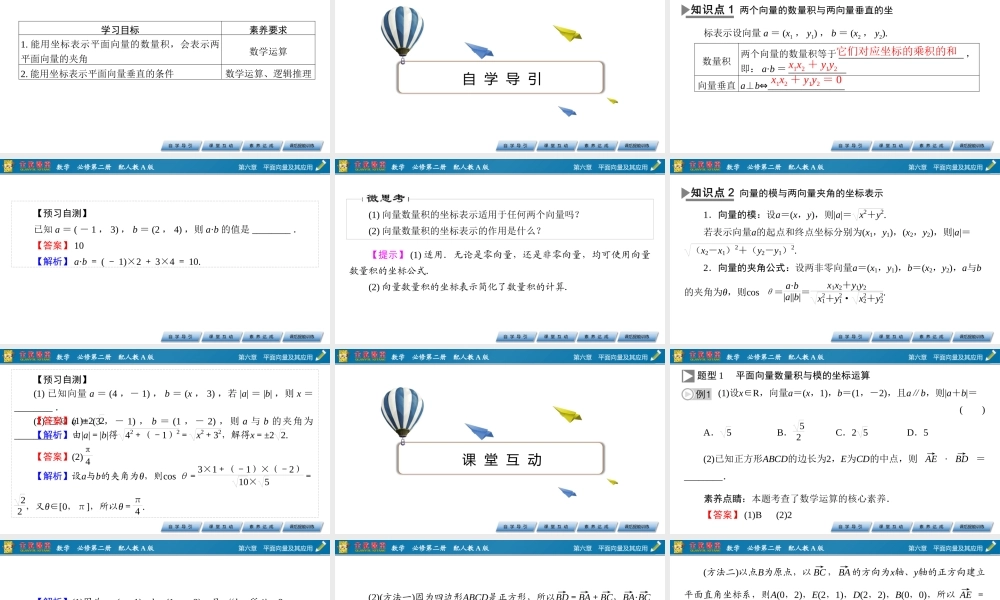
第六章平面向量及其应用6.3平面向量基本定理及坐标表示6.3.5平面向量数量积的坐标表示第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成学习目标素养要求1.能用坐标表示平面向量的数量积,会表示两平面向量的夹角数学运算2.能用坐标表示平面向量垂直的条件数学运算、逻辑推理第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成自学导引第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成标表示设向量a=(x1,y1),b=(x2,y2).两个向量的数量积与两向量垂直的坐数量积两个向量的数量积等于__________________________,即:a·b=____________向量垂直a⊥b⇔________________它们对应坐标的乘积的和x1x2+y1y2x1x2+y1y2=0第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成【预习自测】已知a=(-1,3),b=(2,4),则a·b的值是________.【答案】10【解析】a·b=(-1)×2+3×4=10.第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成(1)向量数量积的坐标表示适用于任何两个向量吗?(2)向量数量积的坐标表示的作用是什么?【提示】(1)适用.无论是零向量,还是非零向量,均可使用向量数量积的坐标公式.(2)向量数量积的坐标表示简化了数量积的计算.第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成向量的模与两向量夹角的坐标表示1.向量的模:设a=(x,y),则|a|=x2+y2.若表示向量a的起点和终点坐标分别为(x1,y1),(x2,y2),则|a|=(x2-x1)2+(y2-y1)2.2.向量的夹角公式:设两非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ,则cosθ=a·b|a||b|=x1x2+y1y2x21+y21·x22+y22.第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成【预习自测】(1)已知向量a=(4,-1),b=(x,3),若|a|=|b|,则x=________.(2)已知a=(3,-1),b=(1,-2),则a与b的夹角为________.【答案】(1)±22【解析】由|a|=|b|得42+(-1)2=x2+32,解得x=±22.【答案】(2)π4【解析】设a与b的夹角为θ,则cosθ=3×1+(-1)×(-2)10×5=22,又θ∈[0,π],所以θ=π4.第六章平面向量及其应用自学导引课堂互动课后提能训练数学必修第二册配人教A版素养达成课堂互动第六章平面向...