第1课时 图形的面积问题.pptVIP免费

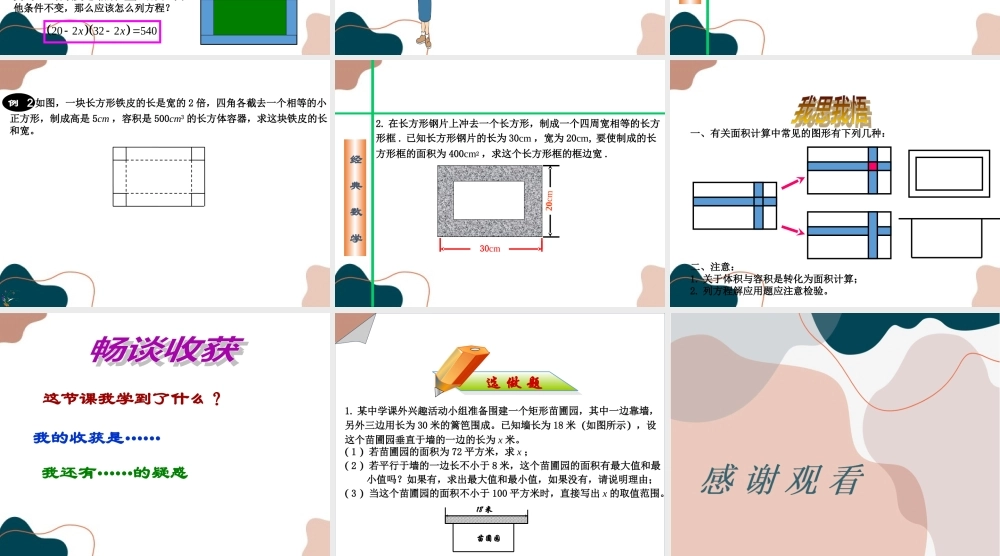
第22章一元二次方程22.3实践与探索第1课时图形的面积问题学校生物小组有一块长32米，宽20米的矩形试验田，为了管理方便，准备沿平行于两边的方向纵横各开辟一条等宽的小道。要使种植面积为540平方米，小道的宽应是多少米？你是怎么考虑的呢？用总的面积减去两条道路的面积加上重叠部分面积等于540.x3220x20x325402x学校生物小组有一块长32米，宽20米的矩形试验田，为了管理方便，准备沿平行于两边的方向纵横各开辟一条等宽的小道。要使种植面积为540平方米，小道的宽应是多少米？解：设道路宽为x米，由题意得：2521000xx540322032202xxx整理得：解得：50221xx，答：小道的宽应是2米。你还有另外的解法吗？我想可以利用平移来解决呢！x（不合题意，舍去）学校生物小组有一块长32米，宽20米的矩形试验田，为了管理方便，准备沿平行于两边的方向纵横各开辟一条等宽的小道。要使种植面积为540平方米，小道的宽应是多少米？解：设道路宽为x米，由题意得：x32x20xx2032540xx2521000xx整理得：解得：50221xx，答：小道的宽应是2米。比较两种解法，哪种更简便？为什么？【技巧】利用“图形经过平移，它的面积大小不会改变”的道理，纵、横两条路移动一下，使列方程容易些（目的是求出路面的宽，至于实施工，仍可按原图的位置修路）（不合题意，舍去）上题中如果改变道路的位置或道路的条数（只列方程），则变式1：若改变道路的位置如右图所示。其他条件不变，那么应该怎么列方程？2032540xx变式2：若改变道路的条数如右图。其他条件不变，那么应该怎么列方程？20322540xx变式3：若改变道路的位置如右图，其他条件不变，那么应该怎么列方程？202322540xx例1如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为a为米15米），围成中间隔有一道篱笆的长方形花圃。aDCBA如果要围成面积为45平方米的花圃，AB的长是多少米？（1）能围成面积比51平方米大的花圃吗？如果能，说明围法；如果不能，请说明理由。（2）※经典数学1.有一面积是150平方米的长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边（门除外）用竹篱笆围成，篱笆总长33米。求鸡场的长和宽各多少米？18米2米例2如图，一块长方形铁皮的长是宽的2倍，四角各截去一个相等的小正方形，制成高是5cm，容积是500cm3的长方体容器，求这块铁皮的长和宽。经典数学2.在长方形...