第1课时 弧长与扇形面积.pptVIP免费

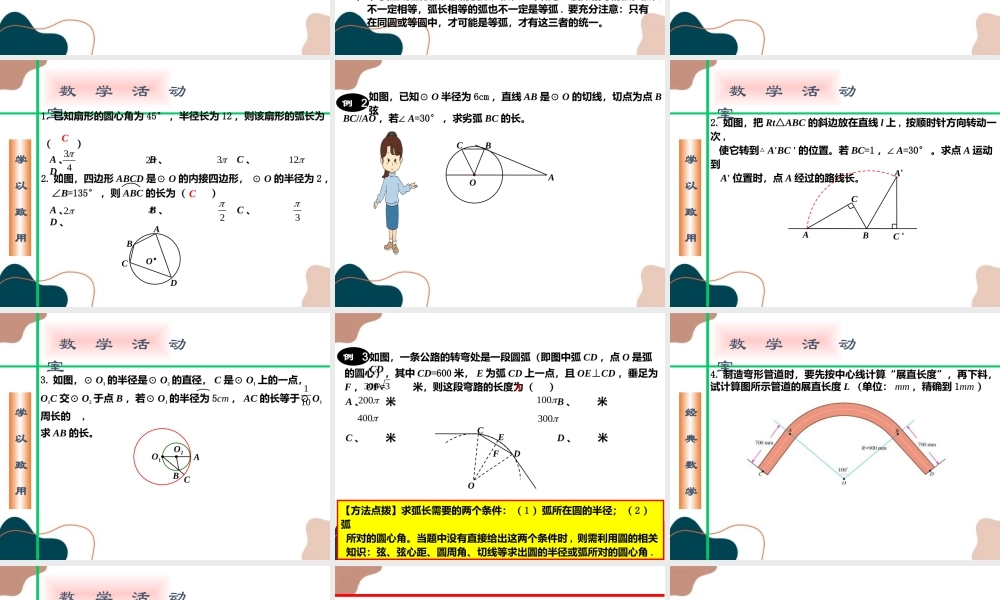
第27章圆27.3圆中的计算问题第1课时弧长与扇形面积（Ⅰ）圆的周长公式：（Ⅱ）圆的面积公式：rrC22rS问题：如图是圆弧形状的铁轨示意图，其中铁轨的半径100m,圆心角为90°,你能求出这段铁轨的长度吗？如果圆心角是任意角度，如何计算它所对的弧长呢？5041002m100我们容易看出这段铁轨是圆周长的41故铁轨的长度为：思考：下图中各圆心角所对的弧长分别是圆周长的几分之几？90°45°n°180°圆心角占整个周角的所对弧长是360180r236018036090r23609036045r236045360nrn2360通过刚才的计算，你有何收获呢？思考：如果弧长为l，圆心角的度数为n，圆的半径为r，那么180rnrnl2360180rnl（1）在弧长公式中，n表示“1°”的圆心角的倍数,在应用公式计算时，“n”和“180”可不写单位；如果弧长为l，圆心角度数为n，圆的半径为r，那么，弧长的计算公式为：180rnl（2）若题目中没有标明精确度，可以用“”表示弧长；（3）要正确区分弧、弧的度数、弧长三个概念：度数相等的弧，弧长不一定相等，弧长相等的弧也不一定是等弧.要充分注意：只有在同圆或等圆中，才可能是等弧，才有这三者的统一。【方法点拨】在弧长公式中有三个未知量：弧长、半径、圆心角的度数,利用弧长公式可解决已知这三个量中的两个量求第三个量的问题。例1若扇形的半径为6，圆心角为120°，则此时扇形的弧长是（）A、B、C、D、3456B41806120l数学活动室学以致用1.已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为（）A、B、C、D、432312A、B、C、D、2232.如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则ABC的长为（）CCOABCD例2如图，已知⊙O半径为6cm，直线AB是⊙O的切线，切点为点B弦BC//AO，若∠A=30°，求劣弧BC的长。BCAO数学活动室学以致用2.如图，把Rt△ABC的斜边放在直线l上,按顺时针方向转动一次,使它转到△A'BC'的位置。若BC=1，∠A=30°。求点A运动到A'位置时，点A经过的路线长。CABC'A'数学活动室学以致用3.如图，⊙O1的半径是⊙O2的直径，C是⊙O1上的一点，O1C交⊙O2于点B，若⊙O1的半径为5cm，AC的长等于⊙O1周长的,求AB的长。101BAO1O2C【方法点拨】求弧长需要的两个条件：（1）弧所在圆的半径；（2）弧所对的圆心角。当题中没有直接给出这两个条件时,则需利用圆的相关知识：弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角.例3如图，一条...