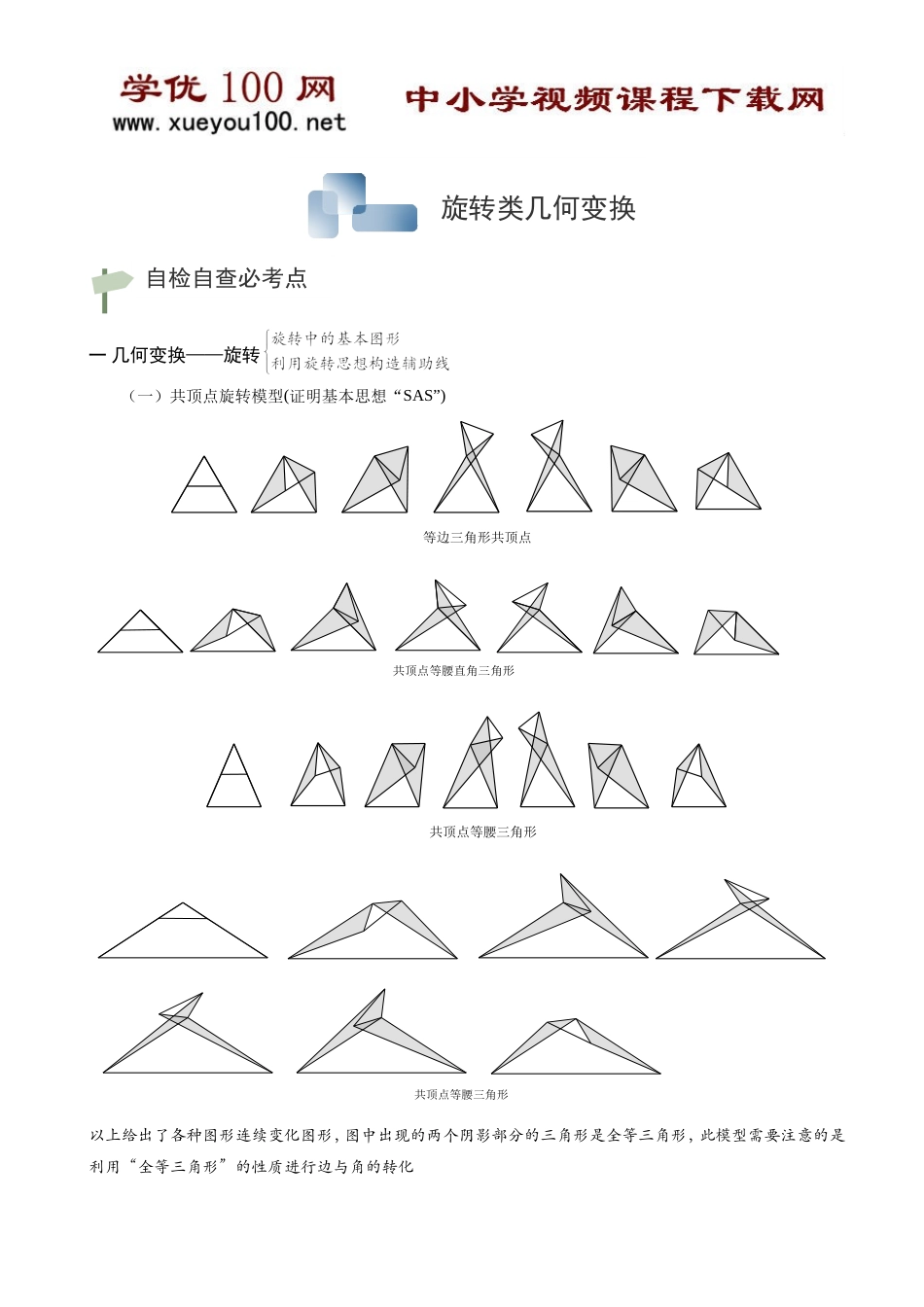
旋转类几何变换一几何变换——旋转(一)共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化自检自查必考点二利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形三旋转变换前后具有以下性质:(1)对应线段相等,对应角相等(2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角.考点一旋转与最短路程☞考点说明:旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题,涉及费马点问题,视学生程度进行选择性讲解。【例1】如图,四边形是正方形,是等边三角形,为对角线上任意一点,将绕点逆时针旋转得到,连接、、.⑴求证:⑵①当点在何处时,的值最小;②当点在何处时,的值最小,并说明理由;⑶当的最小值为时,求正方形的边长.中考满分必做题ENMDCBA【例2】阅读下列材料对于任意的,若三角形内或三角形上有一点,若有最小值,则取到最小值时,点为该三角形的费马点。①若三角形内有一个内角大于或等于,这个内角的顶点就是费马点②若三角形内角均小于,则满足条件时,点既为费马点解决问题:⑴如图,中,三个内角均小于,分别以、为边向外作等边、,连接、交于点,证明:点为的费马点。(即证明)且PEDCBAQABCDEP⑵如图,点为三角形内部异于点的一点,证明:⑶若,,,直接写出的最小值考点二利用旋转求点的坐标☞考点说明:利用全等三角形的性质进行边与角的转化。【例3】正方形在坐标系中的位置如图所示,将正方形绕点顺时针方向旋转后,点的坐标为()A.B.C.D.【例4】如图,在平面直角坐标系中,的顶点的坐标为,若将绕点逆时针旋转后,点到达点,则点的坐标是________DCBAOyxyxBAO考点三旋转与勾股定理☞考点说明:在等边三角形与正方形中,常见的一种题型,应重点掌握【例5】如图,是等边中的一个点,,则的边长是________【例6】如图,在中,,,是内的一点,且,求的度数.【例7】如图点是正方形内部一点,,则=.考点四利用旋转的性质解决几何有关的计算☞考点说明:此类问题多以选择填空的形式出现,较为简单,有的时候也会再综合题中出现。【...