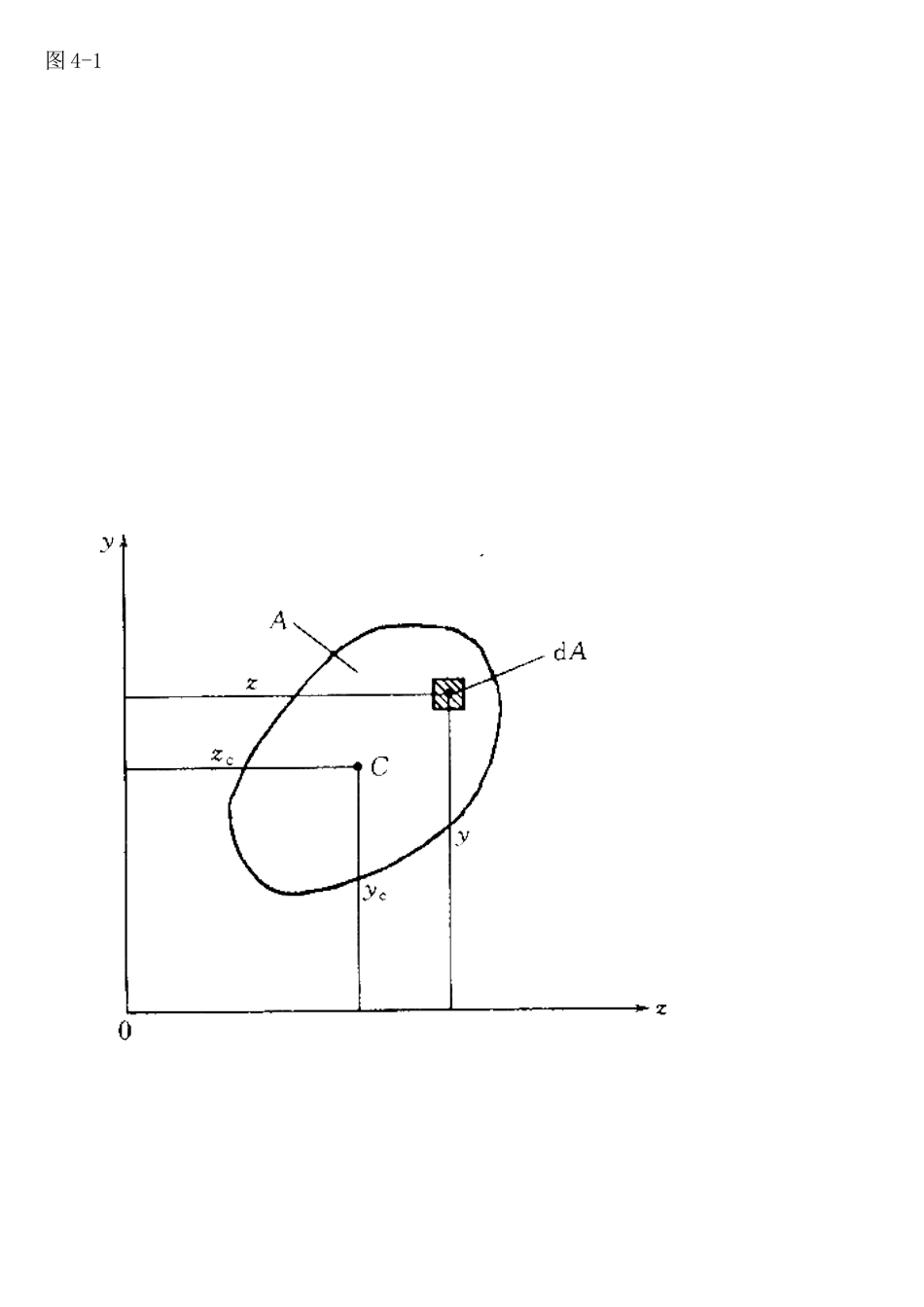
2005年注册岩土工程师考前辅导精讲班材料力学第四讲截面的几何性质【内容提要】本节主要了解静矩和形心、极惯性矩和惯性积的概念,熟悉简单图形静矩、形心、惯性矩和惯性积的计算,掌握其计算公式。掌握惯性矩和惯性积平行移轴公式的应用,熟练掌握有一对称轴的组合截面惯性矩的计算方法。准确理解形心主轴和形心主惯性矩的概念,熟悉常见组合截面形心主惯性矩的计算步骤。【重点、难点】重点掌握平行移轴公式的应用,形心主轴概念的理解和有一对称轴的组合截面惯性矩的计算步骤和方法一、静矩与形心(一)定义设任意截面如图4-1所示,其面积为A,为截面所在平面内的任意直角坐标系。c为截面形心,其坐标为,。则截面对z轴的静矩截面对轴的静矩截面形心的位置(二)特征1.静矩是对一定的轴而言的,同一截面对不同轴的静矩值不同。静矩可能为正,可能为负,也可能为零。2.静矩的量纲为长度的三次方.即。单位为或。3.通过截面形心的坐标称为形心轴。截面对任一形心轴的静矩为零;反之,若截面对某轴的静矩为零,则该轴必通过截面之形心。4.若截面有对称轴,则截面对于对称轴的静矩必为零,截面的形心一定在该对称轴上。5.组合截面(由若干简单截面或标准型材截面所组成)对某一轴的静矩,等于其组成部分对同一轴的静矩之代数和(图4-2),即合截面的形心坐标为:图4-1图4-2二、惯性矩惯性积(一)定义设任意截面如图4-3所示,其面积为A,为截面所在平面内任意直角坐标系。则图4-3截面对轴的惯性矩截面对y轴的惯性矩截面对0点的极惯性矩截面对轴的惯性积(二)特征1.惯性矩是对某一坐标轴而言的.惯性积是对某一对坐标轴而言的,同一截面对不同的坐标轴,其数值不同。极惯性矩是对点(称为极点)而言的,同一截面对不同的点,其值也不相同。惯性矩。极惯性矩恒为正值,而惯性积可能为正,可能为负,也可能为零。2.惯性矩、惯性积、极惯性矩的量纲均为长度的四次方,即。,单位为m4或mm43.对某一点的极惯性矩恒等于以该点为原点的任一对直角坐标轴的惯性矩之和。即4.惯性积是对某一对直角坐标的.若该对坐标中有一轴为截面的对称轴,则截面对这一对坐标轴的惯性积必为零;但截面对某一对坐标轴的惯性积为零,则这对坐标中不一定有截面的对称轴。5.组合截面对某一轴的惯性矩等于其组成部分对同一轴的惯性矩之和。即组合截面对某一对坐标轴的惯性积,等于其组成部分对同一对坐标轴的惯性积之和,即组合截面对某一点的极惯性矩,等于其组成部分对同一点极惯性...