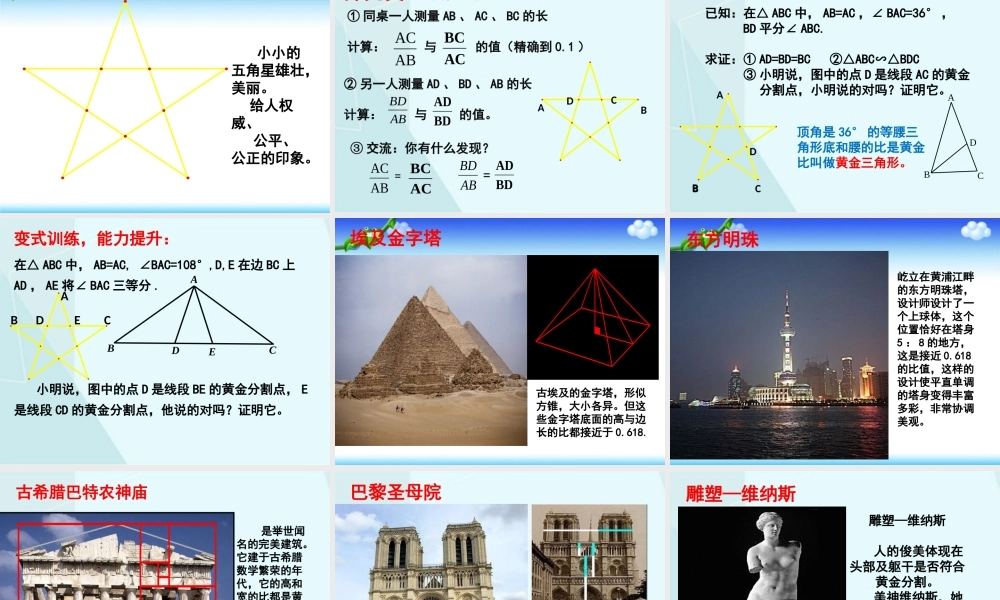
北师大版九年级上册4.4探索三角形相似的条件第4课时黄金分割学习目标1.了解黄金分割的定义,记住黄金数.2.会判断某一点是否一条线段的黄金分割点。认识黄金三角形。3.会用方程思想解决问题,了解黄金分割的文化价值。下列矩形照片,你认为哪一张最美?(1)(2)(3)(1)(2)看电视时,你观察主持人在哪个位置让人感觉更协调,更美观?这两张照片中你认为哪一个人的身材更美?(1)(2)导入新课ACBABCBCA如图,点C把线段AB分成两条线段AC和BC,如果ACABACBC=那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点AC与AB的比叫做黄金比.CABAC2=AB∙BC什么是黄金分割长全短长巧记:或BC与AC的比也叫黄金比一条线段有两个黄金分割点。CABABACACBC=∴点C是线段AB的黄金分割点 点C是线段AB的黄金分割几何语言表示: ABAC=ACBC∴(判定)(性质)1.课本110页用什么方法计算黄金比?黄金比是多少?2.设AB=1AC为X,BC为(1-X)则求得AC=BC=3,若AB=a则AC=aBC=a4.你还能求出哪些量的值?CAB215牢记:=≈0.618215253215253ABAC1.如图:P是线段MN的黄金分割点,则()。2.把长为2cm的线段进行黄金分割,则较长的线段为()cm.3.已知点C是线段AB的一个黄金分割点,则AC:AB为()PMN当堂练习发现美:澳大利亚中国美国新加坡叙利亚越南巴基斯坦摩洛哥朝鲜小小五角星的美:小小的五角星雄壮,美丽。给人权威、公平、公正的印象。探究美:操作思考③交流:你有什么发现?ACBDABACACBC=BDADABBD=①同桌一人测量AB、AC、BC的长计算:与的值(精确到0.1)ABACACBC②另一人测量AD、BD、AB的长计算:与的值。ABBDBDAD应用美:DCBA已知:在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC.求证:①AD=BD=BC②△ABC∽△BDC③小明说,图中的点D是线段AC的黄金分割点,小明说的对吗?证明它。ABCD顶角是36°的等腰三角形底和腰的比是黄金比叫做黄金三角形。BEBDAC在△ABC中,AB=AC,∠BAC=108°,D,E在边BC上AD,AE将∠BAC三等分.小明说,图中的点D是线段BE的黄金分割点,E是线段CD的黄金分割点,他说的对吗?证明它。变式训练,能力提升:BDECA古埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的高与边长的比都接近于0.618.埃及金字塔屹立在黄浦江畔的东方明珠塔,设计师设计了一个上球体,这个位置恰好在塔身5:8的地方,这是接近0.618的比值,这样的设计使平直单调的塔身变得丰富多彩,非常协调美观。东方明珠古希腊巴特农神庙是举世闻名的完美建筑。它建于古希腊数学繁荣的年...