复件 二项分布poission分布（8）(1).pptVIP免费

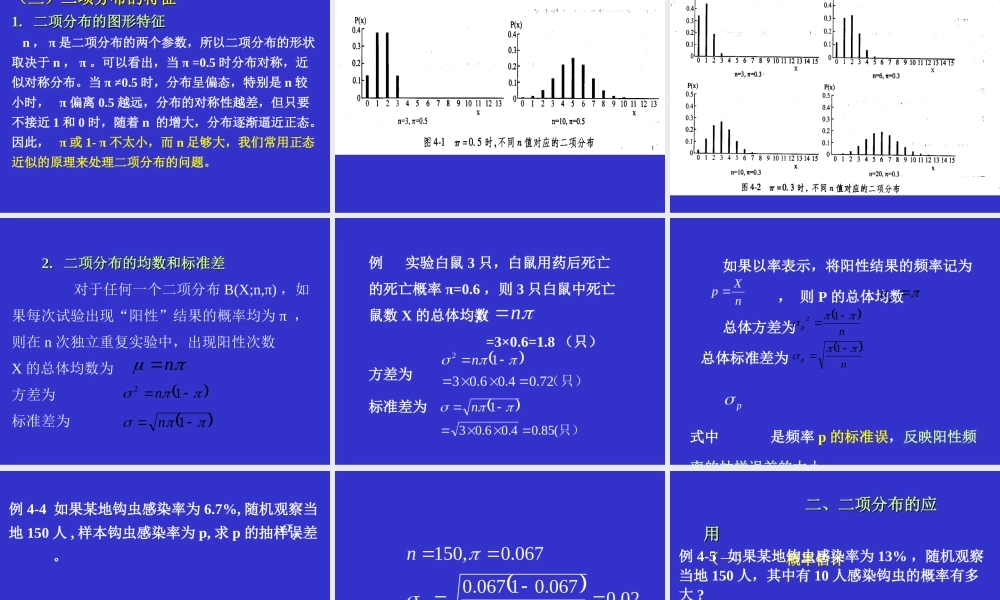
二项分布/possion分布（一）成败型实验（Bernoulli实验）在医学卫生领域的许多实验或观察中，人们感兴趣的是某事件是否发生。如用白鼠做某药物的毒性实验，关心的是白鼠是否死亡；某种新疗法临床实验观察患者是否治愈；观察某指标的化验结果是否呈阳性等。将我们关心的事件A出现称为成功，不出现称为失败，这类试验就称为成-败型实验。指定性资料中的二项分类实验。二项分布一、二项分布的概念与特征成-败型（Bernoulli）实验序列：满足以下三个条件的n次实验构成的序列称为成-败型实验序列。1）每次实验结果，只能是两个互斥的结果之一（A或非A）。2)相同的实验条件下，每次实验中事件A的发生具有相同的概率π。（非A的概率为1-π）。实际工作中要求π是从大量观察中获得的较稳定的数值。3)各次实验独立。各次的实验结果互不影响。（二）二项分布的概率函数二项分布是指在只能产生两种可能结果（如“阳性”或“阴性”）之一的n次独立重复实验中，当每次试验的“阳性”概率保持不变时，出现“阳性”的次数X=0,1,2,…,n的一种概率分布。若从阳性率为π的总体中随机抽取大小为n的样本，则出现“阳性”数为X的概率分布即呈现二项分布，记作B(X;n,π)或B(n,π)。举例设实验白鼠共3只，要求它们同种属、同性别、体重相近，且他们有相同的死亡概率，即事件“白鼠用药后死亡白鼠用药后死亡”为A，相应死亡概率为π。记事件“白鼠用药后不死亡”为，相应不死亡概率为1-π。设实验后3只白鼠中死亡的白鼠数为X，则X的可能取值为0，1，2和3，则死亡鼠数为X的概率分布即表现为二项分布。独立事件的乘法定理互不相容事件的加法定理构成成-败型实验序列的n次实验中，事件A出现的次数X的概率分布为：XnXXnCXP1其中X=0，1，2…，n。n，π是二项分布的两个参数。对于任何二项分布，总有P40例：3.1•应用条件：每一种结果在每次试验中都有恒定的概率，试验之间应是独立的。•N=10,x=37)1(3)(mmmfffffffPnxCxpxnxxn,,2,1,0,)1()(nxnnnxnxxnnnnnnxpnpxppppCCCC0011100)()()()2()1()0()1()1()1()1()]1([nxCxpxnxxn,,2,1,0,)1()(1)1(因为：所以：1)]1([)(0nxnxp009766.02)21()21()!110(!0!10)0(10100p0097656.0)2(10)21)(21()!110(!1!10)1(109p0439453.0)2(...