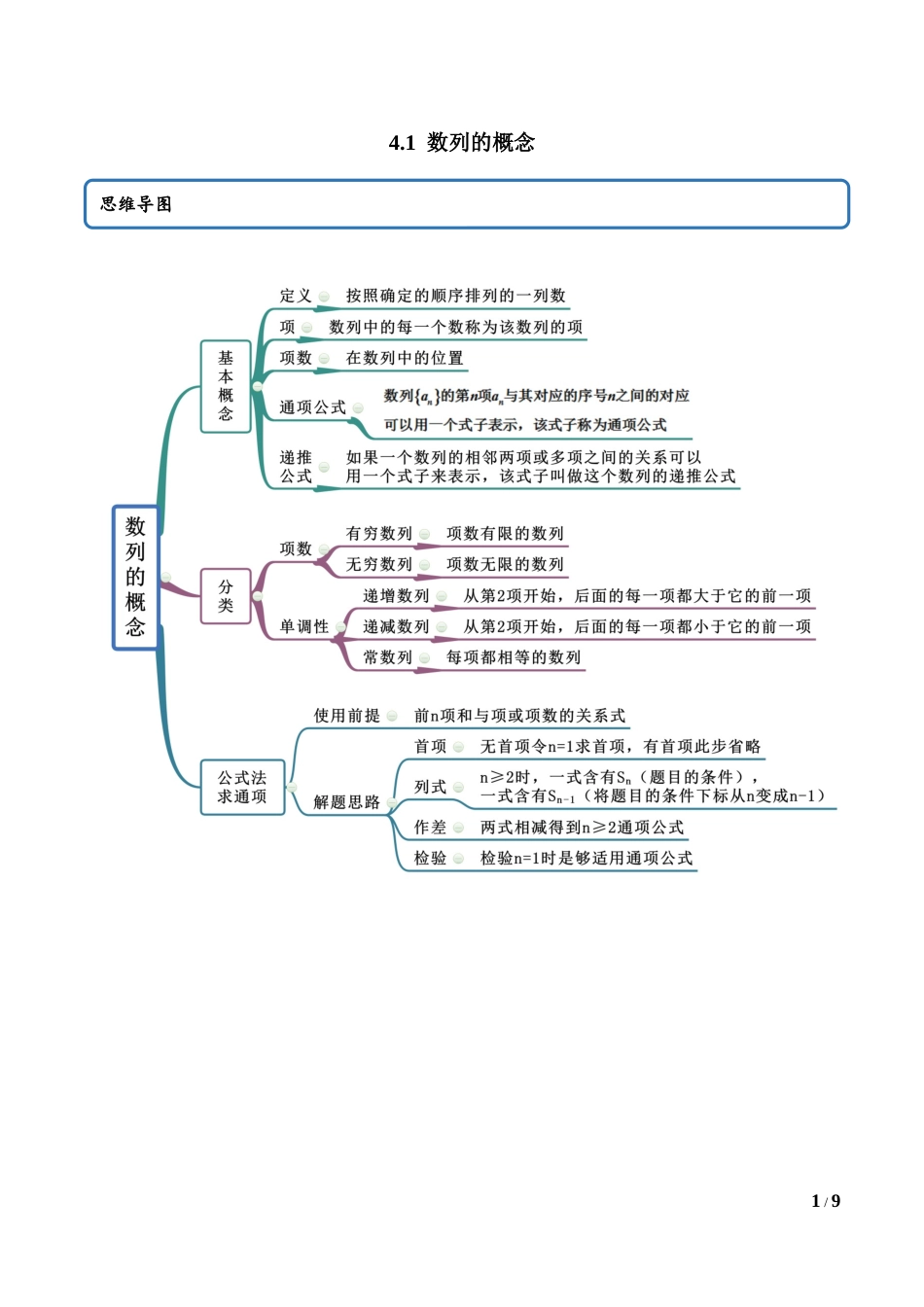
1/94.1数列的概念思维导图2/9考法一根据通项求项【例1】(2020·宜宾市南溪区第二中学校)已知数列,则数列的第4项为()A.B.C.D.【答案】B【解析】依题意.故选:B.【一隅三反】1.(2020·陕西省商丹高新学校期末(文))若数列的通项公式为,则()A.27B.21C.15D.13【答案】A常见考法3/9【解析】因为,所以,故选:A.2.(2020·定远县育才学校月考)已知数列,1,,,,…,,…,则是它的().A.第22项B.第23项C.第24项D.第28项【答案】B【解析】因为题中数列的第项为,而,所以是题中数列的第23项.故选:B.3.(2020·安徽高一期末)已知数列的通项公式为,则的值是()A.9B.13C.17D.21【答案】C【解析】把n=5代入=4n-3中得到所求为17.故选C.考法二根据项写通项公式【例2】(2020·邵东县第一中学月考)数列的一个通项公式为()A.B.C.D.【答案】C【解析】数列1,-3,5,-7,9,…的一个通项公式.故选C.【一隅三反】1.(2020·四川金牛·成都外国语学校高一开学考试(理))数列,3,,,…,则是这个数列的第()A.8项B.7项C.6项D.5项【答案】C4/9【解析】列,3,,,,可化为:数列,,,,,则数列的通项公式为:,当时,则,解得:,故是这个数列的第6项.故选:C.2(2020·玉龙纳西族自治县田家炳民族中学高一期中)若数列的前项分别是、、、,则此数列一个通项公式为()A.B.C.D.【答案】A【解析】设所求数列为,可得出,,,,因此,该数列的一个通项公式为.故选:A.3.(2020·辽源市第五中学校高一期中(文))数列3,7,13,21,31,…的通项公式是()A.B.C.D.不存在【答案】C【解析】依题意可知,所以.故选:C考法三根据递推公式求项【例3】(2020·湖南省长沙县第九中学期末)数列满足,(为正整数,),则()A.43B.28C.16D.7【答案】C5/9【解析】因为,(为正整数,),令,所以;令,所以.故选:C.【一隅三反】1.(2020·安徽期末)在数列中,,,则()A.-2B.1C.D.【答案】C【解析】因为,,所以,,,所以数列是周期为3的周期数列,所以.故选:C2.(2020·福建厦门·期末)已知数列满足,,则()A.B.C.D.【答案】C【解析】因为,所以解得.故选:C6/93.(2020·广西玉林·期末)在数列中,,,则()A.-2B.2C.1D.-1【答案】B【解析】 ,,∴,,则数列是周期为2的周期数列,故.故选:B.4.(2020·辽源市田家炳高级中学校高一期末(文))数列中,若,,则(...