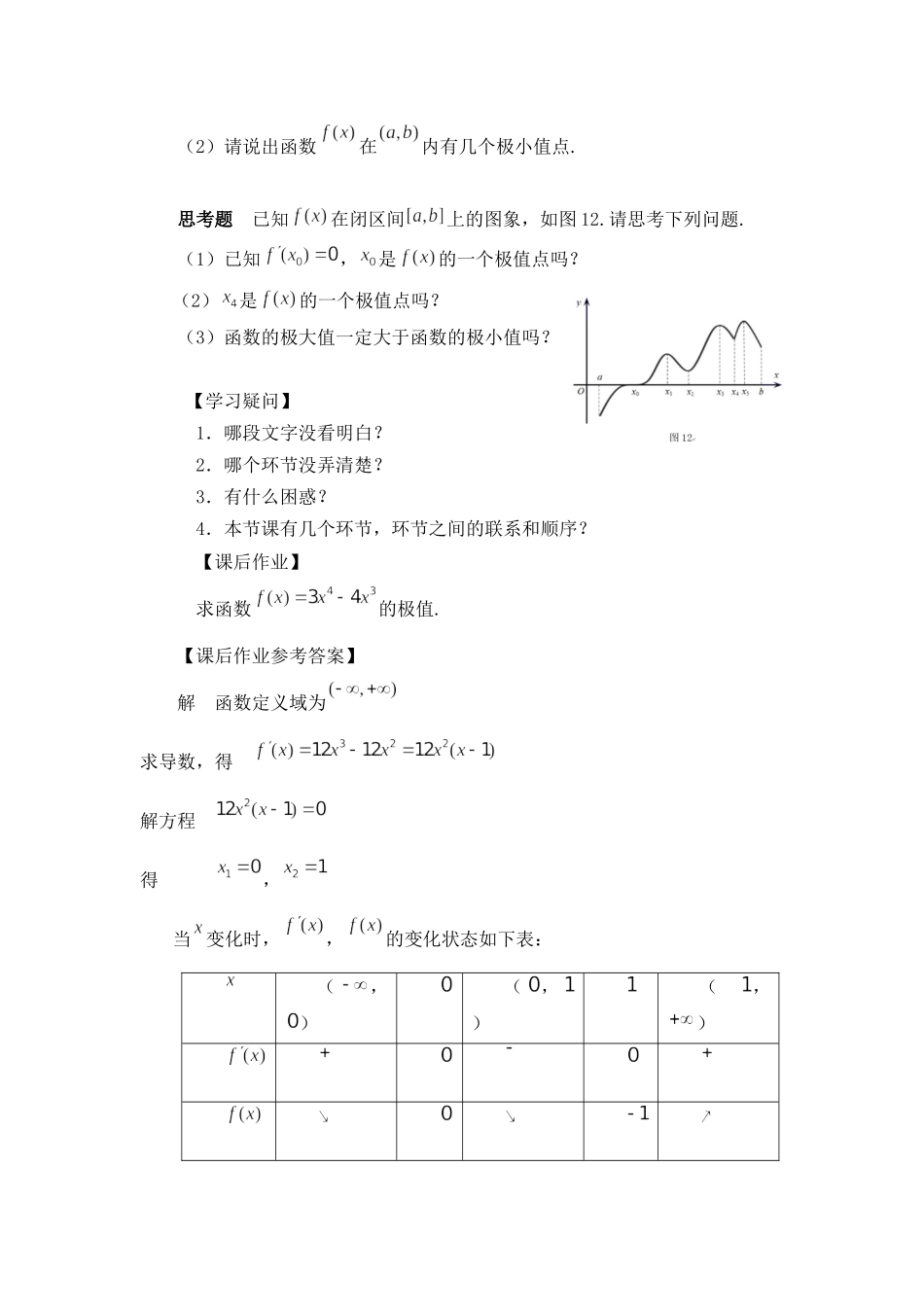
《利用导数研究函数极值》(1)学习任务单【学习目标】1.结合函数实例,借助几何直观感知并经历函数极值概念的形成过程,提升数学抽象概括能力.2.结合函数实例,归纳并掌握求解函数极值的步骤,提升逻辑推理能力.3.在具体实例中,运用恰当的方法解决函数极值的简单问题,提升数学转化能力,逻辑推理和数学运算能力.【课上任务】问题1观察下列函数图象(图1-图3),请说出图中的点、、、、有什么共同的特点?在数学上,我们称这样的点的函数值为函数的极值.在这三个函数的图象中,点、、对应的函数值、、,都比附近点的函数值小,我们称之为极小值;点、对应的函数值、,都比附近点的函数值大,我们称之为极大值.问题2还能再列举出一个有上述类似特征的函数吗?问题3根据前面的分析,你能试着给出函数极大值与极小值的定义吗?问题4已知函数在闭区间上的图象,如图5.观察图象,请回答下列问题.(1)请说出函数的极值点;(2)请说出函数在每一个极值点处的导数值;(3)请说出在极大值点与极小值点附近函数及其导数的取值情况.图6例已知函数.求函数的极值,试着作出函数的图象.思考与总结(1)求函数的极值.(2)求可导函数极值的步骤:I确定函数定义域,求导函数;II求方程(导函数等于0)在定义域内的所有实数根;III对每个实数根进行检验,判断在每个根的左右两侧,导函数的符号如何变化.如果的符号由正变负,则是极大值;如果的符号由负变正,则是极小值.追问:方程的实数根一定是函数的极值点吗?例已知函数的导函数的图象,如图10.观察导函数的图象,请说出的极值.练习已知函数的定义域为,导函数在上的图象,如图11.(1)请说出函数在内有几个极大值点;(2)请说出函数在内有几个极小值点.思考题已知在闭区间上的图象,如图12.请思考下列问题.(1)已知,是的一个极值点吗?(2)是的一个极值点吗?(3)函数的极大值一定大于函数的极小值吗?【学习疑问】1.哪段文字没看明白?2.哪个环节没弄清楚?3.有什么困惑?4.本节课有几个环节,环节之间的联系和顺序?【课后作业】求函数的极值.【课后作业参考答案】解函数定义域为求导数,得解方程得,当变化时,,的变化状态如下表:(,)(,)(,)从表上看出,当时,函数有极小值;函数无极大值.