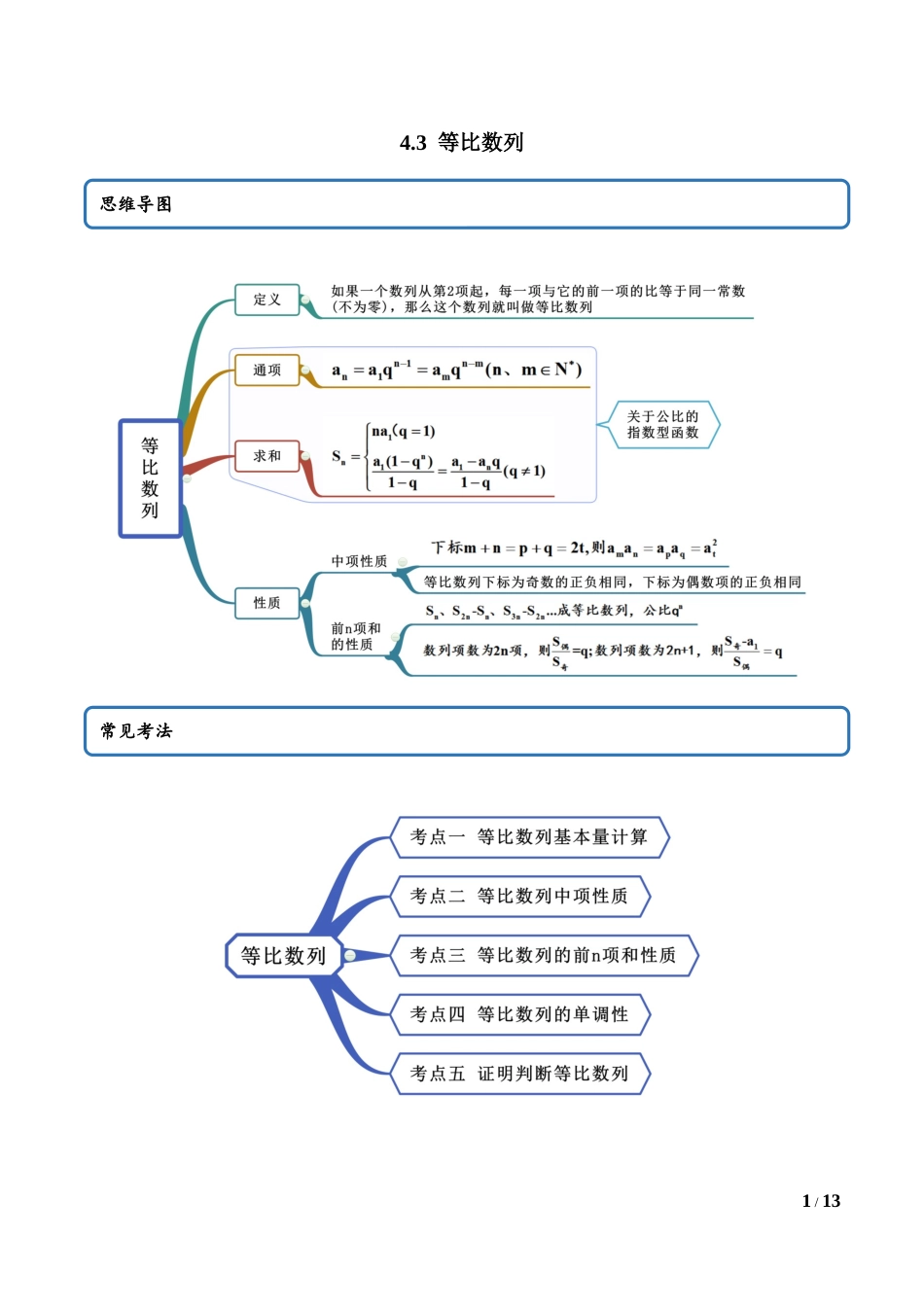
1/134.3等比数列思维导图常见考法2/13考点一等比数列基本量计算【例1】(1)(2020·四川仁寿一中开学考试)在等比数列中,,,则公比的值为()A.B.或1C.-1D.或-1(2)(2020·哈密市第十五中学月考)已知各项均为正数的等比数列的前4项和为15,且,则()A.16B.8C.4D.2(3)(2020·四川省内江市第六中学开学考试(理))等比数列的前项和,则=()A.-1B.3C.-3D.1【答案】(1)B(2)C(3)C【解析】(1)由题意,解得或.故选:B.【答案】C(2)设正数的等比数列{an}的公比为,则,解得,,故选C.(3)因为数列是等比数列故满足,,代入得到故答案选C.【一隅三反】3/131.(2020·石嘴山市第三中学月考)已知是等比数列,a1=2,a4=,则公比q=()A.B.-2C.2D.【答案】D【解析】 是等比数列,∴,∴.故选:D.2.(2020·黑龙江工农·鹤岗一中高一期末(文))已知数列满足,若,则等于A.1B.2C.64D.128【答案】C【解析】因为数列满足,所以该数列是以为公比的等比数列,又,所以,即;故选C.3.(2020·合肥市第十一中学高二开学考试)各项都是正数的等比数列中,成等差数列,则公比的值为()A.B.C.D.或【答案】B【解析】由题得,所以,4/13因为是各项都是正数的等比数列,所以,所以.故选:B4.(2020·全国高二月考(文))已知各项均为正数的等比数列,且成等差数列,则的值是()A.B.C.D.【答案】D【解析】各项均为正数的等比数列的公比设为q,则q>0,由成等差数列,可得,即,所以,解得或(舍),所以.故选:D.5.(2020·贵州省思南中学月考)设正项等比数列的前项和为,,则公比等于()A.B.C.D.【答案】A【解析】因为,所以所以,即5/13因为,所以故选:A考点二等比数列中项性质【例2】(1)(2020·自贡市田家炳中学开学考试)等比数列的各项均为正数,且,则()A.B.C.D.(2)(2020·河南高二月考)在等比数列中,若,则()A.B.C.D.【答案】(1)B(2)B【解析】(1)由等比数列的性质可得:,所以.则故选B.(2)由等比中项的性质可得,解得,因此,.故选:B.【一隅三反】1.(2020·安徽滁州·期末)在等比数列中,是方程的根,则A.B.C.D.【答案】A【解析】由题得所以,因为,所以所以.故答案为A6/132.(2019·福建高三学业考试)若三个数1,2,m成等比数列,则实数()A.8B.4C.3D.2【答案】B【解析】因为为等比数列,故即,故选:B.3.(2020·宁夏二模(理))已知实数成...