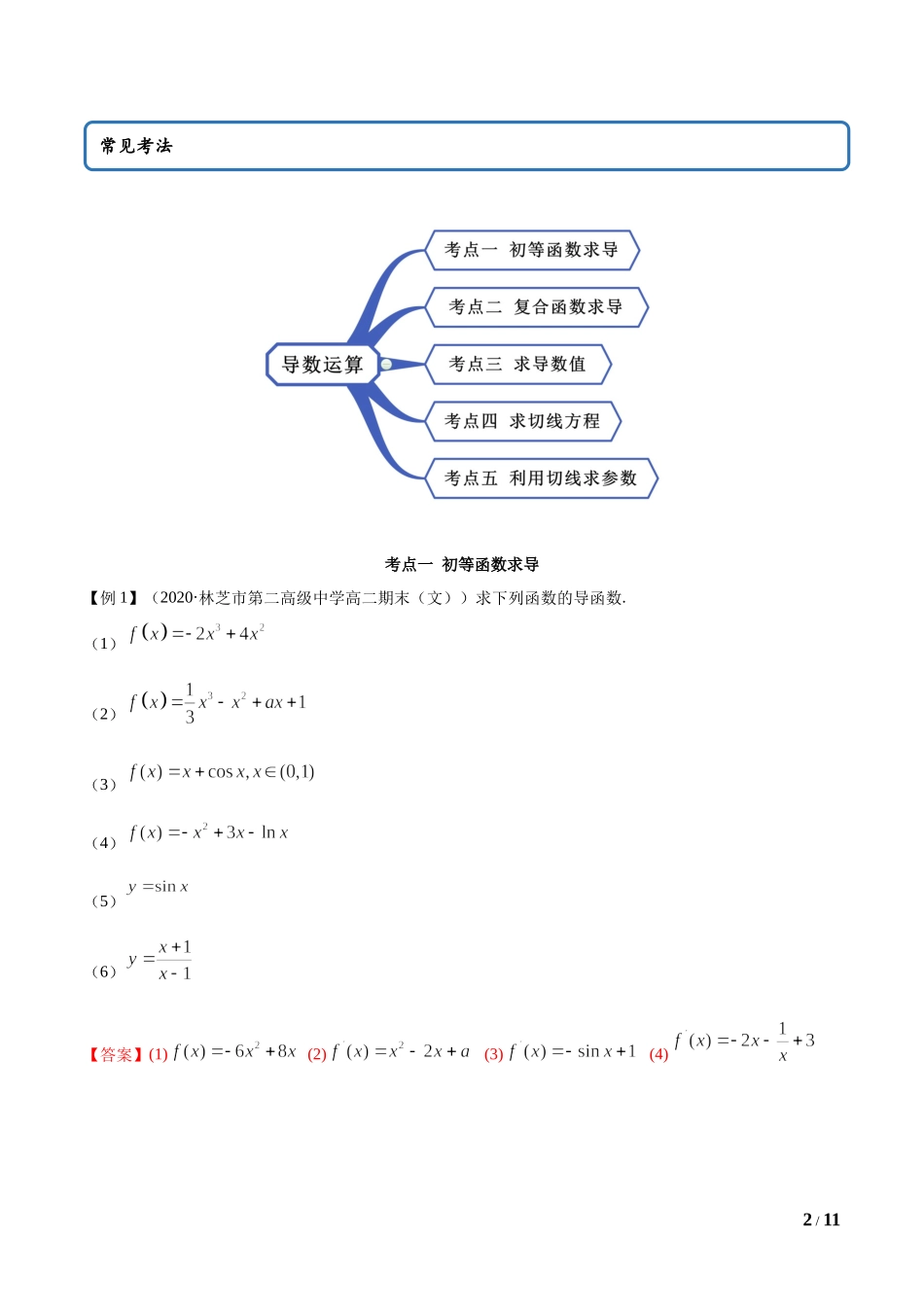
1/115.2导数的运算思维导图2/11考点一初等函数求导【例1】(2020·林芝市第二高级中学高二期末(文))求下列函数的导函数.(1)(2)(3)(4)(5)(6)【答案】(1)(2)(3)(4)常见考法3/11(5)(6)【解析】(1)由,则;(2)由,则;(3)由,则;(4)由,则;(5)由,则;(6)由,则.【一隅三反】1.(2020·西藏高二期末(文))求下列函数的导数.(1);(2);(3).【答案】(1)(2)(3)【解析】(1)(2)(3)4/112.(2020·通榆县第一中学校高二月考(理))求下列函数的导数:(Ⅰ);(Ⅱ).【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)由导数的计算公式,可得.(Ⅱ)由导数的乘法法则,可得.3.(2020·山东师范大学附中高二期中)求下列函数在指定点的导数:(1),;(2),.【答案】(1)(2)【解析】(1),(2),考点二复合函数求导【例2】.(2020·凤阳县第二中学高二期末(理))求下列函数的导数:(1);(2).【答案】(1);(2)或.【解析】(1);5/11(2).或.【一隅三反】1.(2020·陕西碑林·西北工业大学附属中学高二月考(理))求下列函数的导数:(1);(2);(3);(4).【答案】(1);(2);(3);(4).【解析】(1);(2);(3) ∴;(4).2.(2020·横峰中学高二开学考试(文))求下列各函数的导数:(1);(2)(3)y=【答案】(1);(2).(3)【解析】(1)因为令,6/11所以(2).(3)令,则,所以;考点三求导数值【例3】.(2020·甘肃城关·兰州一中高二期中(理))已知函数的导函数为,且满足,则A.B.C.D.【答案】A【解析】,求导得,则,解得.故选:A.【一隅三反】1.(2020·广东湛江·高二期末(文))已知函数,则()A.B.C.D.【答案】A7/11【解析】,,因此,.故选:A.2.(2020·四川高二期中(理))若函数,则的值为()A.0B.C.D.【答案】B【解析】因为,所以令,则,所以,则,故选:B.3.(2020·广西桂林·高二期末(文))已知函数,则()A.3B.0C.2D.1【答案】A【解析】由题得.故选:A考点四求切线方程【例4】.(2020·郸城县实验高中高二月考(理))已知曲线(1)求曲线在点处的切线方程;(2)求曲线过点的切线方程【答案】(1);(2)或.【解析】(1) ,∴在点处的切线的斜率,∴曲线在点处的切线方程为,即.8/11(2)设曲线与过点的切线相切于点,则切线的斜率,∴切线方程为,即. 点在该切线上,∴,即,∴,∴,∴,解得或.故所求切...