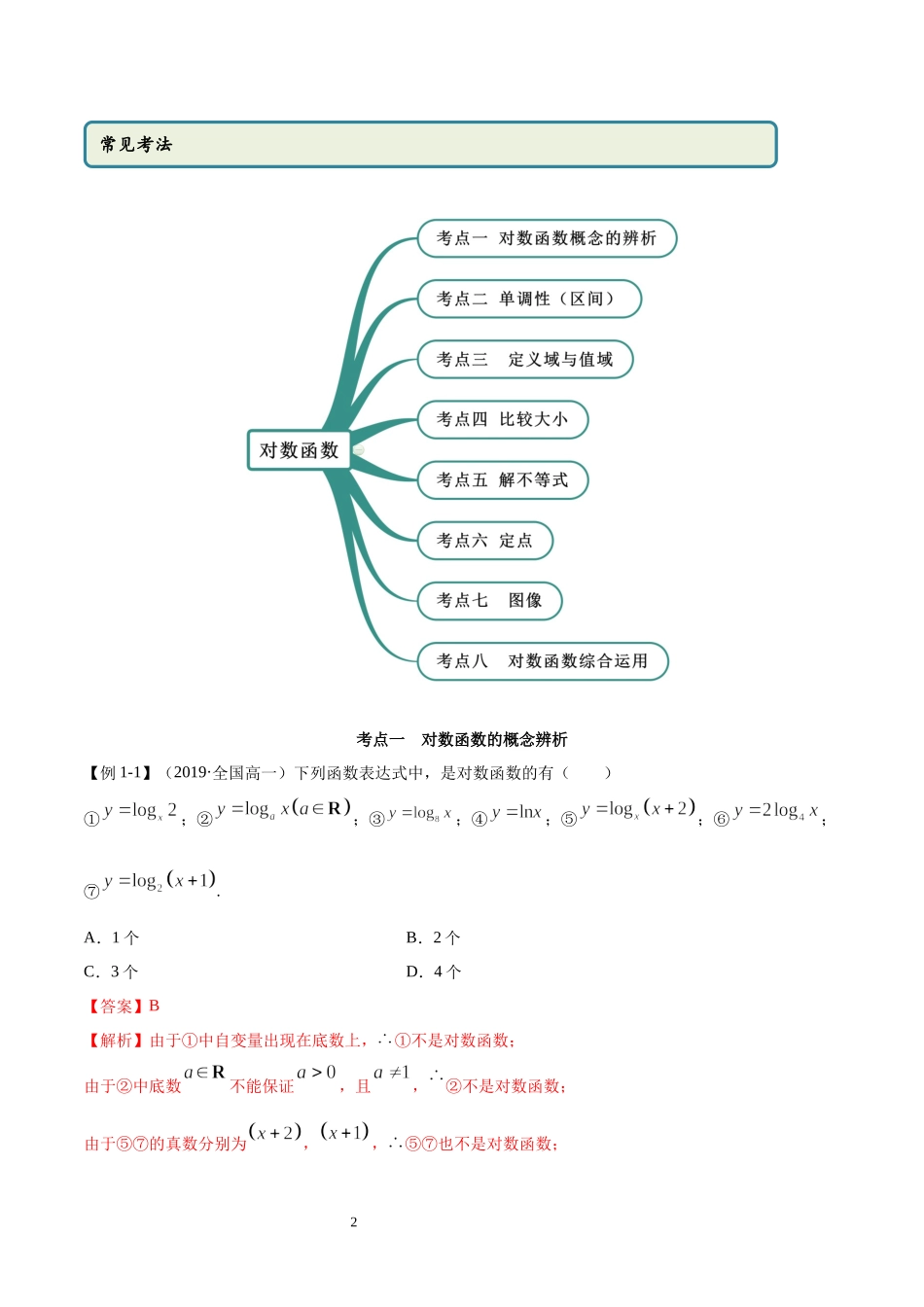
14.4对数函数思维导图2考点一对数函数的概念辨析【例1-1】(2019·全国高一)下列函数表达式中,是对数函数的有()①;②;③;④;⑤;⑥;⑦.A.1个B.2个C.3个D.4个【答案】B【解析】由于①中自变量出现在底数上,①不是对数函数;由于②中底数不能保证,且,②不是对数函数;由于⑤⑦的真数分别为,,⑤⑦也不是对数函数;常见考法3由于⑥中的系数为2,⑥也不是对数函数;只有③④符合对数函数的定义.故选:B【例1-2】(2020·宝鸡市渭滨中学高一期中)若函数的图像过点,则的值为()A.B.2C.D.【答案】B【解析】由题,.故选:B【一隅三反】1.(2020·全国高一课时练习)下列函数为对数函数的是()A.y=logax+1(a>0且a≠1)B.y=loga(2x)(a>0且a≠1)C.y=log(a-1)x(a>1且a≠2)D.y=2logax(a>0且a≠1)【答案】C【解析】根据对数函数的定义,可得判定,只有函数且复数对数函数的概念,所以函数且是对数函数,而选项A、B、D中的函数只能是对数型函数,不是对数函数.故选:C.2.下列函数是对数函数的是()A.B.判断一个函数是对数函数的方法4C.D.【答案】C【解析】由对数函数定义可以,本题选C.3.下列函数,是对数函数的是A.y=lg10xB.y=log3x2C.y=lnxD.y=log(x–1)【答案】C【解析】由对数函数的定义,形如y=logax(a>0,a≠1)的函数是对数函数,由此得到:y=lg10x=x,y==2、y=都不是对数函数,只有y=lnx是对数函数.故选C.4.(2020·全国高一课时练习)对数函数的图象过点M(16,4),则此对数函数的解析式为()A.y=log4xB.y=xC.y=xD.y=log2x【答案】D【解析】由于对数函数的图象过点M(16,4),所以4=loga16,得a=2所以对数函数的解析式为y=log2x,故选D.考点二单调性(区间)【例2】(1)(2020·辽宁锦州·高二期末)函数的单调减区间是()A.B.C.D.(2)(2019·四川省新津中学高一月考)已知在上是增函数,则实数的取值范围是()A.B.C.D.5【答案】(1)D(2)C【解析】由题:,,解得:,的减区间,即的减区间,对称轴为结合二次函数单调性,所以的减区间.故选:D(2)设,在上是增函数,,即,解得,实数的取值范围是,故选:C.【一隅三反】1.(2019·小店·山西大附中高一期中)函数的单调递减区间为()A.B.C.D.【答案】A【解析】因为,所以,解得或令,因为的图像开口向上,对称轴方程为,所以内函数在上单调递增,外函数单调递减,所以由复合函数单调性的性质可知函数的单调递减区间...