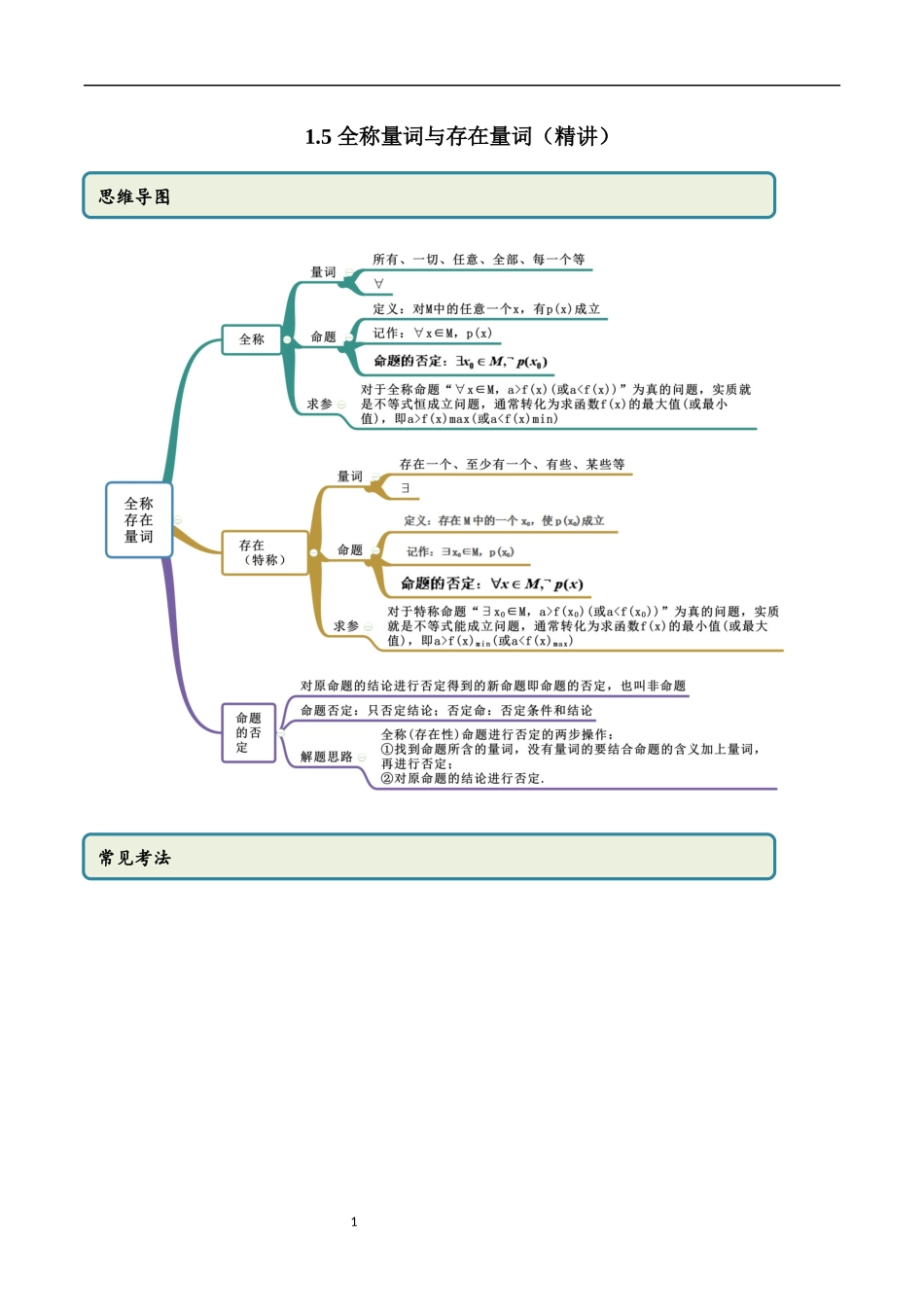
11.5全称量词与存在量词(精讲)思维导图常见考法2考点一全称命题的判断【例1】(2020·全国高一课时练习)下列命题含有全称量词的是()A.某些函数图象不过原点B.实数的平方为正数C.方程有实数解D.素数中只有一个偶数【答案】B【解析】“某些函数图象不过原点”即“存在函数,其图象不过原点”;“方程有实数解”即“存在实数,使”;“素数中只有一个偶数”即“存在一个素数,它是偶数”,这三个命题都是存在量词命题,“实数的平方为正数”即“所有的实数,它的平方为正数”,是全称量词命题,其省略了全称量词“所有的”,所以正确选项为B.【一隅三反】1.(2020·全国高一)下列语句不是全称量词命题的是()A.任何一个实数乘以零都等于零B.自然数都是正整数C.高一(一)班绝大多数同学是团员D.每一个实数都有大小【答案】C【解析】A中命题可改写为:任意一个实数乘以零都等于零,故A是全称量词命题;B中命题可改写为:任意的自然数都是正整数,故B是全称量词命题;C中命题可改写为:高一(一)班存在部分同学是团员,C不是全称量词命题;由全称命题的定义,全称命题应包含所有,任意的…等表示全部元素都满足的语句3D中命题可改写为:任意的一个实数都有大小,故D是全称量词命题.故选:C.2.(2020·全国高一单元测试)(多选)下列命题中,是全称量词命题的有()A.至少有一个x使成立B.对任意的x都有成立C.对任意的x都有不成立D.存在x使成立E.矩形的对角线垂直平分【答案】BCE【解析】A和D中用的是存在量词“至少有一个”“存在”,属存在量词命题;B和C用的是全称量词“任意的”,属全称量词命题,所以B、C是全称量词命题;E中命题“矩形的对角线垂直平分”省略量词“任意”,是全称量词命题.故选:BCE考点二特称命题的判断【例2】(2020·全国高一)指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假.(1)∀x∈N,2x+1是奇数;(2)存在一个x∈R,使=0;(3)对任意实数a,|a|>0;【答案】(1)是全称量词命题;是真命题;(2)是存在量词命题;是假命题;(3)是全称量词命题;是假命题.【解析】(1)是全称量词命题.因为都是奇数,所以该命题是真命题.(2)是存在量词命题.因为不存在,使成立,所以该命题是假命题.(3)是全称量词命题.因为,所以不都成立,因此,该命题是假命题.【一隅三反】1.(2020·全国高一课时练习)下列命题中:①有些自然数是偶数;②正方形是菱形;③能被6整除的数4也能被3整除;④...