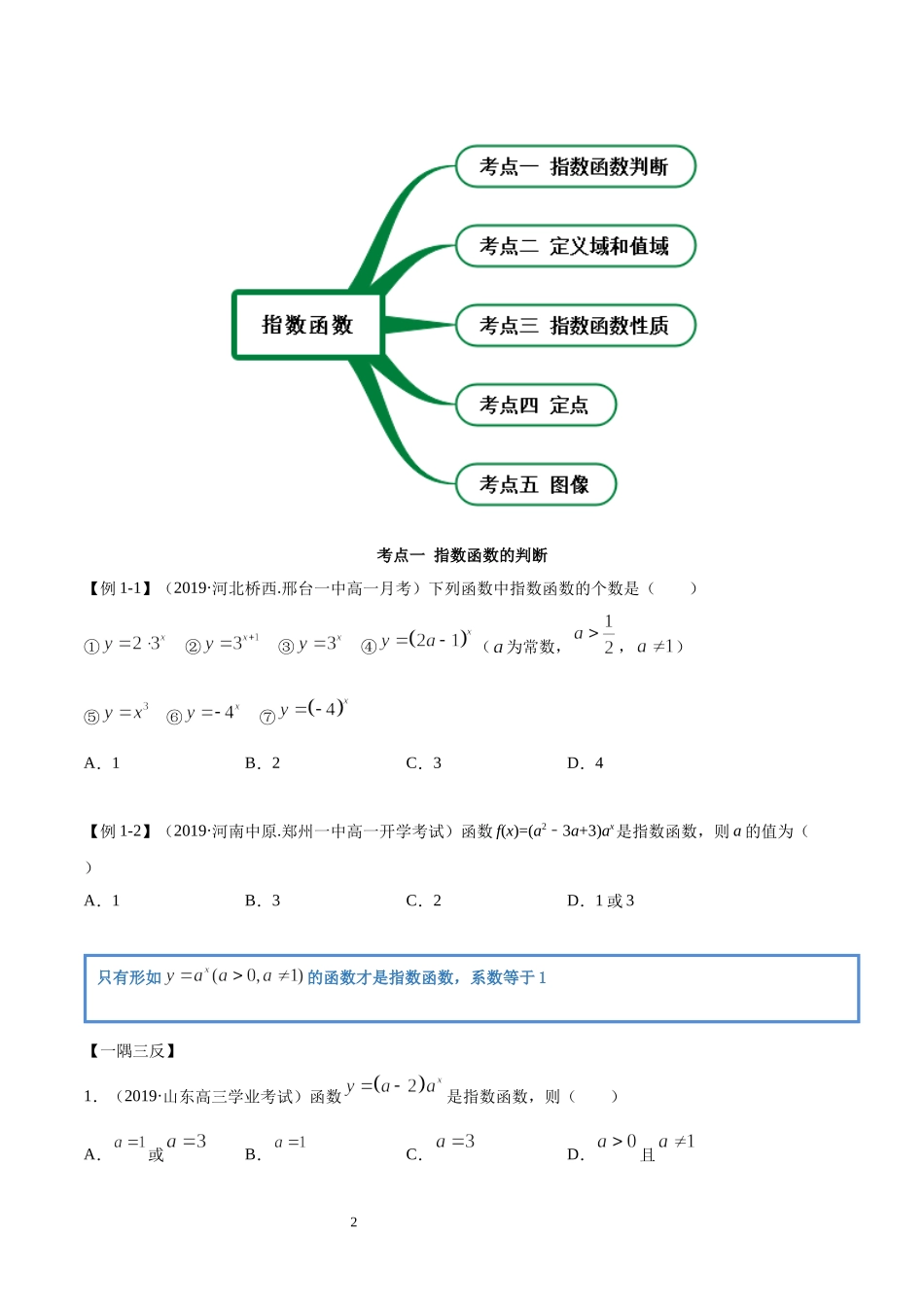
14.2指数函数思维导图常见考法2考点一指数函数的判断【例1-1】(2019·河北桥西.邢台一中高一月考)下列函数中指数函数的个数是()①②③④(为常数,,)⑤⑥⑦A.1B.2C.3D.4【例1-2】(2019·河南中原.郑州一中高一开学考试)函数f(x)=(a23﹣a+3)ax是指数函数,则a的值为()A.1B.3C.2D.1或3【一隅三反】1.(2019·山东高三学业考试)函数是指数函数,则()A.或B.C.D.且只有形如的函数才是指数函数,系数等于132.(2019·呼和浩特开来中学高一期中)若函数是指数函数,则的值为()A.2B.-2C.D.3.(2019·辽宁葫芦岛.高一月考)下列函数不是指数函数的是()A.B.C.D.考点二定义域和值域【例2-1】(2020·全国高一课时练习)求下列函数的定义域和值域:(1);(2);(3).【例2-2】(2018·湖南开福.长沙一中高一月考)若函数的值域为[0,+∞),则实数a的取值范围是_____.4【一隅三反】1.(2020·全国高一课时练习)求下列函数的定义域和值域;(1);(2);(3).2.(2020·全国高一课时练习)求下列函数的定义域与值域.(1)(2)且(3)(4)1.对于y=af(x)这类函数,①定义域是指使f(x)有意义的x的取值范围.②值域问题,应分以下两步求解:ⅰ由定义域求出u=f(x)的值域;ⅱ利用指数函数y=au的单调性或利用图象求得此函数的值域.2.对于y=(ax)2+b·ax+c这类函数,①定义域是R.②值域可以分以下两步求解:ⅰ设t=ax,求出t的范围;ⅱ利用二次函数y=t2+bt+c的配方法求函数的值域.53.(2020·河北新华.石家庄二中高二期末)若函数的值域为,则a的取值范围为()A.B.C.D.4.(2020·云南五华.昆明一中高三其他(理))设函数的定义域为A,函数的值域为B,则()A.B.C.D.5.(2019·湖南高一期中)若函数有最大值,则实数的值为()A.B.C.D.考点三指数函数性质【例3】(1)(2020·贵溪市实验中学高二期末(文))若函数单调递增,则实数a的取值范围是()A.B.C.D.(2)(2019·湖南岳阳楼.岳阳一中高一期中)已知函数,则不等式的解6集为()A.B.C.D.(3)(2019·湖北襄阳)如果,那么()A.B.C.D.【一隅三反】1.(2019·浙江南湖.嘉兴一中高一月考)函数为增函数的区间是()A.B.C.D.2.(2019·浙江柯城.衢州二中高三一模)已知定义在R上的函数m为实数)为偶函数,1.指数函数性质记忆口诀指数增减要看清,抓住底数不放松;反正底数大于0,不等于1已表明;底数若是大于1,图象从下往...