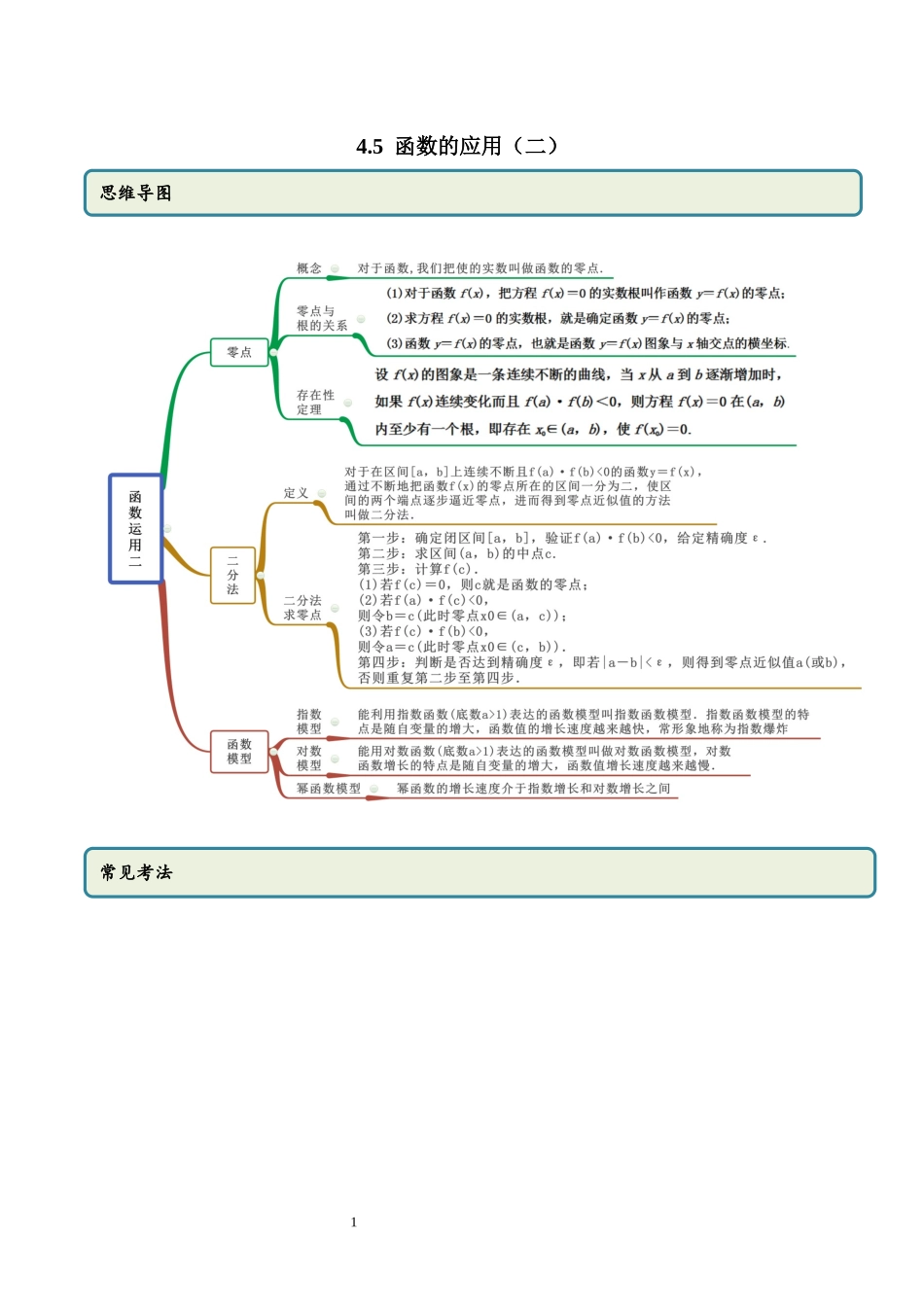
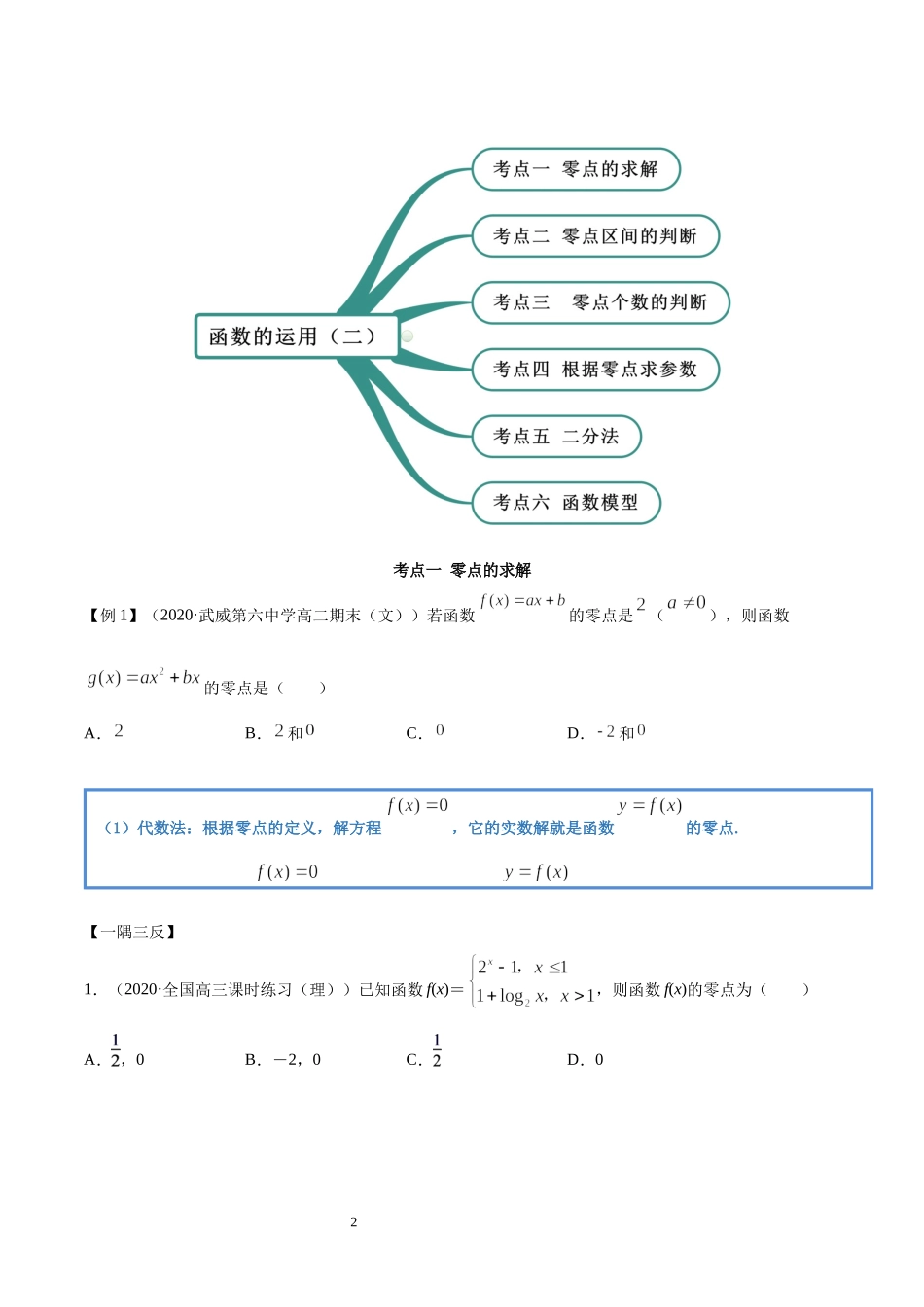
14.5函数的应用(二)思维导图常见考法2考点一零点的求解【例1】(2020·武威第六中学高二期末(文))若函数的零点是(),则函数的零点是()A.B.和C.D.和【一隅三反】1.(2020·全国高三课时练习(理))已知函数f(x)=,则函数f(x)的零点为()A.,0B.-2,0C.D.0(1)代数法:根据零点的定义,解方程,它的实数解就是函数的零点.(2)几何法:若方程无法求解,可以根据函数的性质及图象求出零点.32.已知函数,则函数的零点为________.考点二零点区间的判断【例2】(2020·湖南娄底·高二期末)函数的零点所在的区间为()A.B.C.D.【一隅三反】1.(2020·宁县第二中学高二期中(文))函数f(x)=的零点所在的一个区间是A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)2.(2020·甘肃省岷县第一中学高二月考(文))函数的零点所在区间为()A.B.C.D.3.(2020·浙江衢州·高一期末)函数的零点所在的区间是()A.B.C.D.考点三零点个数的判断判断函数零点所在区间的三个步骤(1)代入:将区间端点值代入函数求出函数的值.(2)判断:把所得的函数值相乘,并进行符号判断.(3)结论:若符号为正且函数在该区间内是单调函数,则在该区间内无零点,若符号为负且函数连续,则在该区间内至少有一个零点.4【例3】(1)(2020·哈尔滨市第十二中学校高二期末(文))函数的零点个数为()A.0个B.1个C.2个D.3个(2)(2020·山东省枣庄市第十六中学高一期中)方程的实数解的个数为()A.1B.2C.3D.0【一隅三反】1.(2020·四川内江·高三三模(理))函数的零点个数为_______.2.(2020·浙江高一课时练习)方程的实根的个数为________.3.已知,则函数的零点的个数为______.考点四根据零点求参数【例4】.(2020·山西应县一中高二期中(文))已知关于的方程有两个不等实根,则实数的取值范围是()判断函数零点个数的三种方法(1)方程法:若方程f(x)=0的解可求或能判断解的个数,可通过方程的解来判断函数是否存在零点或判定零点的个数.(2)图象法:由f(x)=g(x)-h(x)=0,得g(x)=h(x),在同一坐标系内作出y1=g(x)和y2=h(x)的图象,根据两个图象交点的个数来判定函数零点的个数.(3)定理法:函数y=f(x)的图象在区间[a,b]上是一条连续不断的曲线,由f(a)·f(b)<0即可判断函数y=f(x)在区间(a,b)内至少有一个零点.若函数y=f(x)在区间(a,b)上是单调函数,则函数f(x)在区间(a,b)内只有一个零点.5A.B.C.D.【一...