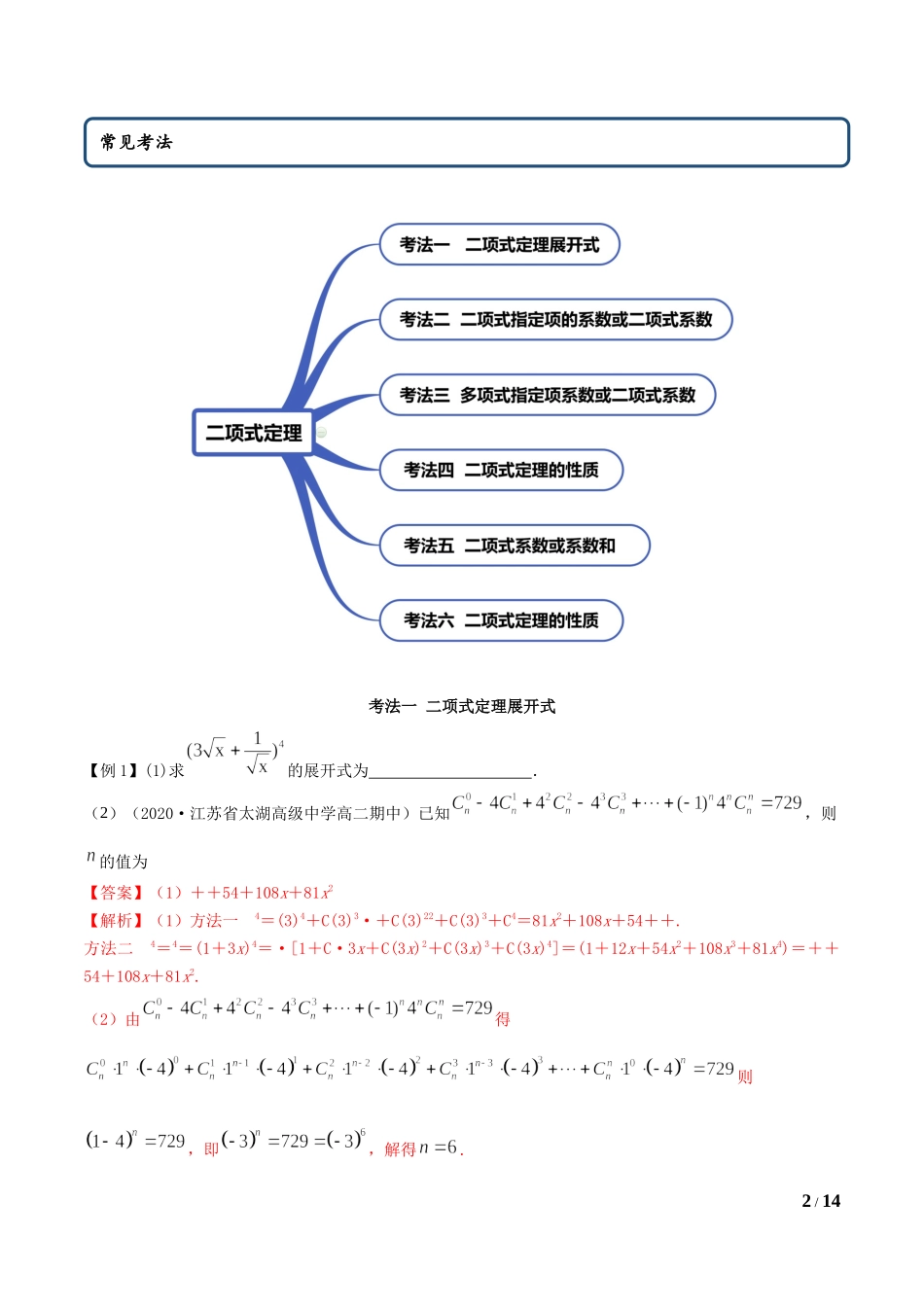
1/146.3二项式定理(精讲)思维导图2/14考法一二项式定理展开式【例1】(1)求的展开式为.(2)(2020·江苏省太湖高级中学高二期中)已知,则的值为【答案】(1)++54+108x+81x2【解析】(1)方法一4=(3)4+C(3)3·+C(3)22+C(3)3+C4=81x2+108x+54++.方法二4=4=(1+3x)4=·[1+C·3x+C(3x)2+C(3x)3+C(3x)4]=(1+12x+54x2+108x3+81x4)=++54+108x+81x2.(2)由得则,即,解得.常见考法3/14【一隅三反】1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是()A.(2x+2)5B.2x5C.(2x-1)5D.32x5【答案】D【解析】依题意可知,多项式的每一项都可看作,故为的展开式,化简.故选D.2.(2020·江苏宿迁市·宿迁中学高二期中)化简:_________.【答案】【解析】则所以故答案为:.考法二二项式指定项的系数与二项式系数【例2】(1)(2020·全国高二单元测试)在(x-)10的展开式中,x6的系数是(2)(2020·广东佛山市·高二期末)二项式的展开式中常数项是______(用数字作答)(3)(2020·安徽省蚌埠第三中学高二月考)的有理项共有项【答案】(1)9(2)70(3)6【解析】(1)由Tk+1=x10-k(-)k,令10-k=6,解得k=4,∴系数为(-)4=94/14(2)二项式的展开式的通项公式,令,得,则常数项为,故答案为:70(3)的通项公式为:,,,,所以有理项共有6项,故选:C【一隅三反】1.(2020·北京市鲁迅中学高二月考)二项式的展开式中的常数项是_______.(用数字作答)【答案】60【解析】有题意可得,二项式展开式的通项为:令可得,此时.2.(2021·上海青浦区)在二项展开式中,常数项是_______.【答案】60【解析】展开式的通项公式是,当时,.故答案为605/143..(2020·青海西宁市)若的展开式中的系数为7,则实数=______.【答案】【解析】根据二项展开式的通项公式可得:,令,可得,,解得:,故答案为:4.(2020·梁河县)已知的展开式的常数项是第7项,则________.【答案】8【解析】根据题意,可知第7项为,而常数项是第7项,则,故.故答案为:8.考法三多项式系数或二项式系数【例3】(1)(2020·福建三明市·高二期末)的展开式中常数项是()A.-252B.-220C.220D.252(2).(2021·四川成都市)若的展开式中常数项为,则()A.B.C.D.【答案】(1)A(2)C【解析】(1)由,可得二项式的展开式通项为,令,解得,所以展开式的常数项为.故选:A.6/14(2)的展开式的通项公...