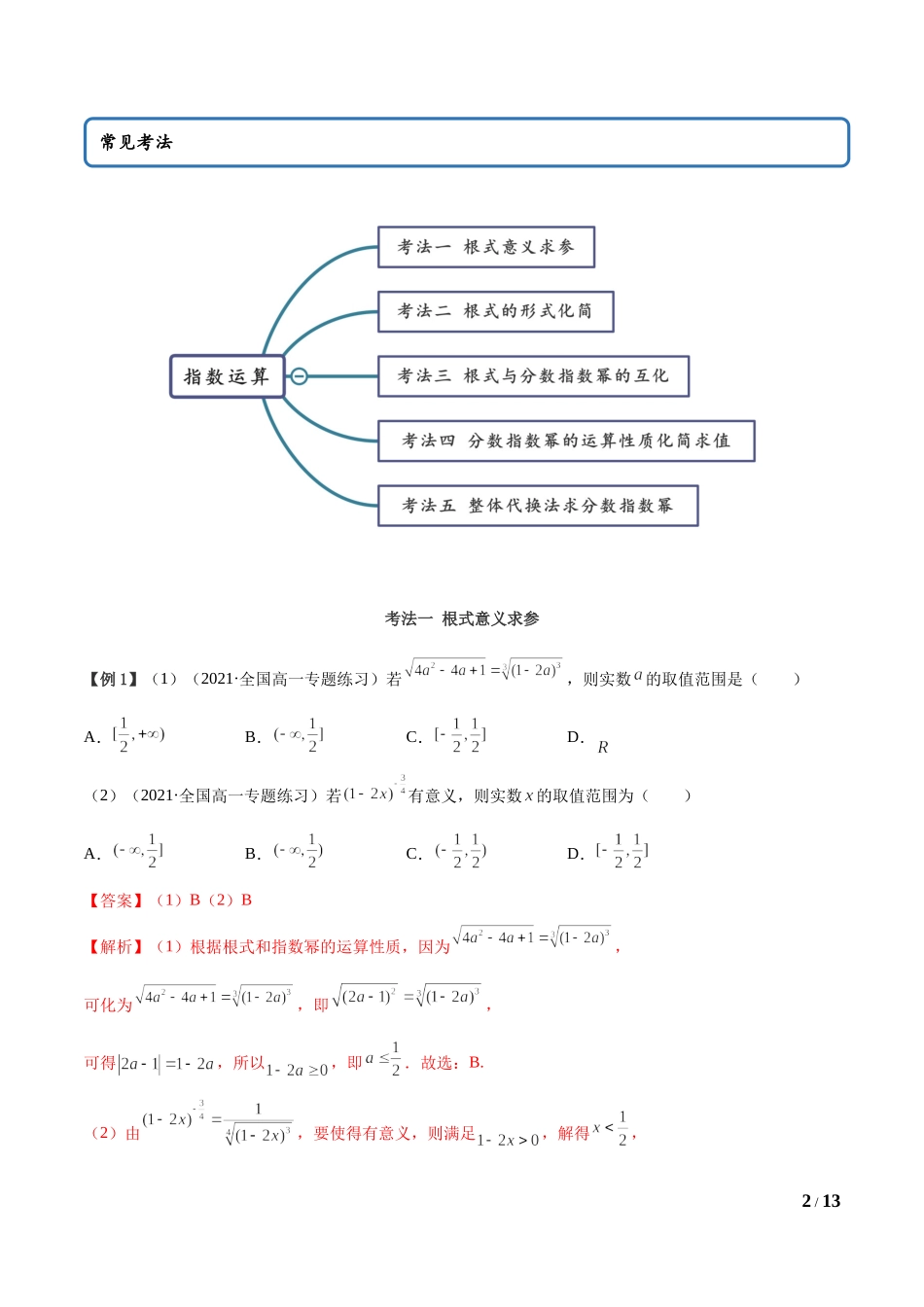
1/134.1指数运算(精讲)思维导图2/13考法一根式意义求参【例1】(1)(2021·全国高一专题练习)若,则实数的取值范围是()A.B.C.D.(2)(2021·全国高一专题练习)若有意义,则实数的取值范围为()A.B.C.D.【答案】(1)B(2)B【解析】(1)根据根式和指数幂的运算性质,因为,可化为,即,可得,所以,即.故选:B.(2)由,要使得有意义,则满足,解得,常见考法3/13即实数的取值范围为.故选:B.【一隅三反】1.(2021·全国高一课时练习)若xn=a(x≠0),则下列说法中正确的个数是()①当n为奇数时,x的n次方根为a;②当n为奇数时,a的n次方根为x;③当n为偶数时,x的n次方根为±a;④当n为偶数时,a的n次方根为±x.A.1B.2C.3D.4【答案】B【解析】n为奇数时,a的n次方根只有1个,为x;当n为偶数时,由于(±x)n=xn=a,所以a的n次方根有2个,为±x.所以说法②④是正确的,故选:B.2.(2021·上海高一专题练习)在①,②,③,④中,n∈N*,a∈R时各式子有意义的是()A.①②B.①③C.②③④D.①②④【答案】B【解析】由>0知①有意义;由<0知②无意义;③中开奇数次方根,所以有意义;当a<0时,a5<0,此时④无意义.故选:B.考点二根式的形式化简【例2】(1)(2021·上海高一专题练习)若,则化简的结果是()A.B.C.D.(2)(2021·全国高一课时练习)若代数式有意义,则()A.B.C.D.(3)(2020·上海)化简:①;4/13②)【答案】(1)B(2)B(3)①;②).【解析】(1)因为,所以,所以.故选:B.(2)由有意义,得解得.所以所以.故选:B.(3)①原式.②原式,即【一隅三反】1.(2021·全国)若,则等于()A.B.C.D.非以上答案【答案】B【解析】因为,所以,原式.故选:B.2.(2021·上海闵行)当时,=___________.5/13【答案】【解析】由,则,故答案为:3.(2021·全国高一课时练习)化简-(-30);(2)(x>0);(3)(b>0).【答案】(1);(2);(3).【解析】(1)原式====.(2)原式======.6/13(3)原式===.【一隅三反】1.(2021·全国高一课时练习)下...