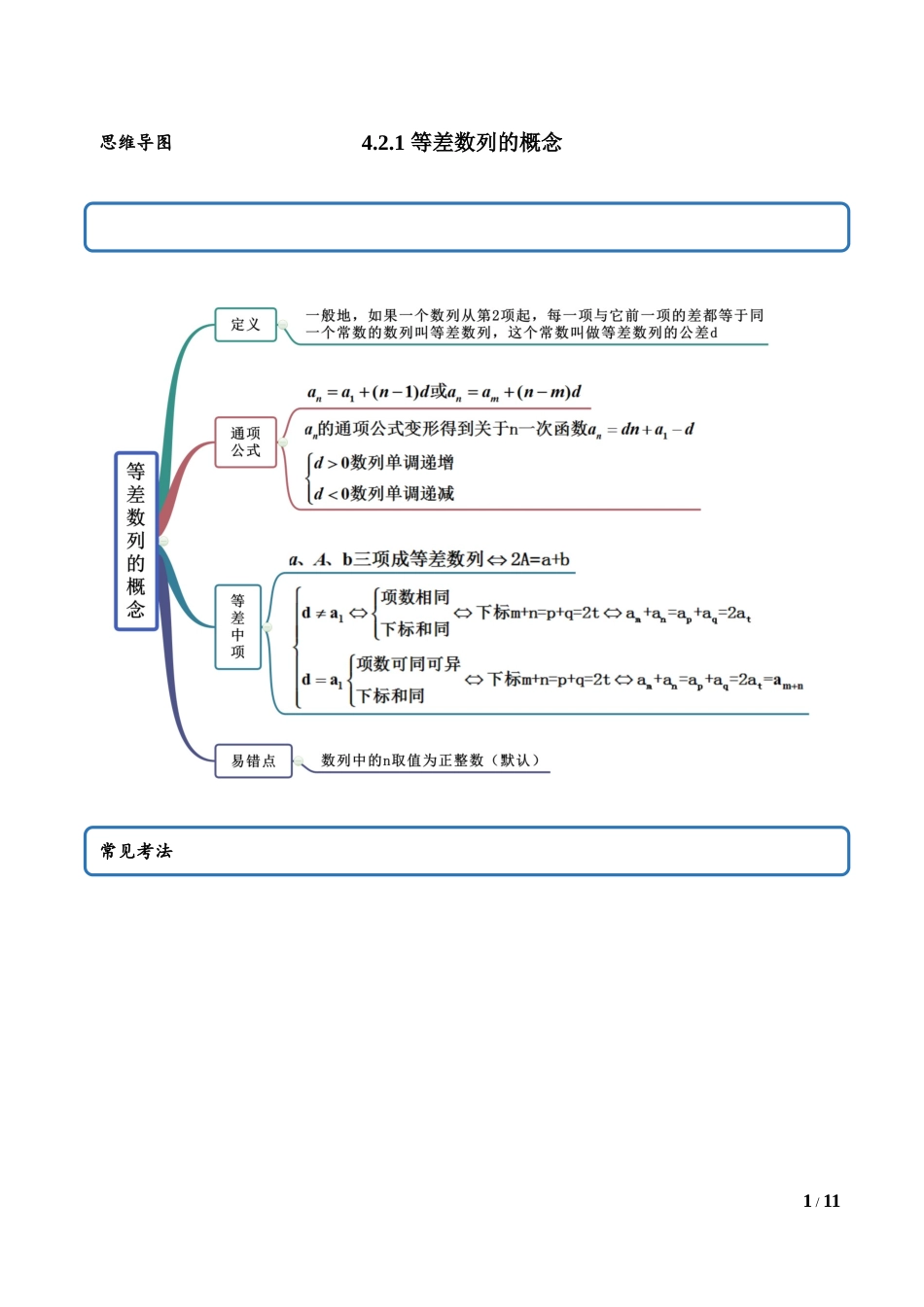
1/114.2.1等差数列的概念思维导图常见考法2/11考点一判断是否为等差数列【例1】(2020·上海高二课时练习)下列数列中,不是等差数列的是()A.1,4,7,10B.C.D.10,8,6,4,2【答案】C【解析】根据等差数列的定义,可得:A中,满足(常数),所以是等差数列;B中,(常数),所以是等差数列;C中,因为,不满足等差数列的定义,所以不是等差数列;D中,满足(常数),所以是等差数列.故选:C.【一隅三反】1.(2019·山西应县一中期末(理))若是等差数列,则下列数列中也成等差数列的是()根据等差数列的定义,只需任意相邻的后一项与前一项的差为定值即可3/11A.B.C.D.【答案】C【解析】A:=(an+an+1)(an+1a﹣n)=d[2a1+(2n1﹣)d],与n有关系,因此不是等差数列.B:==与n有关系,因此不是等差数列.C:3an+13a﹣n=3(an+1a﹣n)=3d为常数,仍然为等差数列;D:当数列{an}的首项为正数、公差为负数时,{|an|}不是等差数列;故选:C2.(2020·全国高一课时练习)已知下列各数列,其中为等差数列的个数为()①4,5,6,7,8,…②3,0,-3,0,-6,…③0,0,0,0,…④…A.1B.2C.3D.4【答案】C【解析】第一个数列是公差为的等差数列.第二个数列是摆动数列,不是等差数列.第三个是公差为的等差数列.第四个是公差为的等差数列.故有个等差数列,所以选C.3.(2020·全国课时练习)已知数列,c为常数,那么下列说法正确的是()A.若是等差数列时,不一定是等差数列B.若不是等差数列时,一定不是等差数列C.若是等差数列时,一定是等差数列D.若不是等差数列时,一定不是等差数列【答案】D【解析】当是等差数列时,由等差数列的性质可知,一定是等差数列,A错;4/11对于数列:1,2,4,5,令,则为等差数列,B错;当c为0时,0,0,0,0是等差数列,但不是等差数列,C错.故选D.考点二求等差数列的项或通项【例2】(1)(2020·兴安县第三中学期中)由=4,确定的等差数列,当an=28时,序号等于()A.9B.10C.11D.12(2)(2020·广西南宁三中开学考试)在单调递增的等差数列中,若,,则()A.B.C.0D.【答案】(1)A(2)C【解析】(1)因为,,所以,所以,解得故选:A(2)因为是等差数列,所以,,解得:,故选:C【一隅三反】1.(2020·江苏江都·邵伯高级中学月考)等差数列中,,,则()A.2B.5C.11D.13【答案】A【解析】因为,得①,又,得②,5/11由①②得:,故.故选:A.2.(2020·兴安县第三中学期中)在数列...