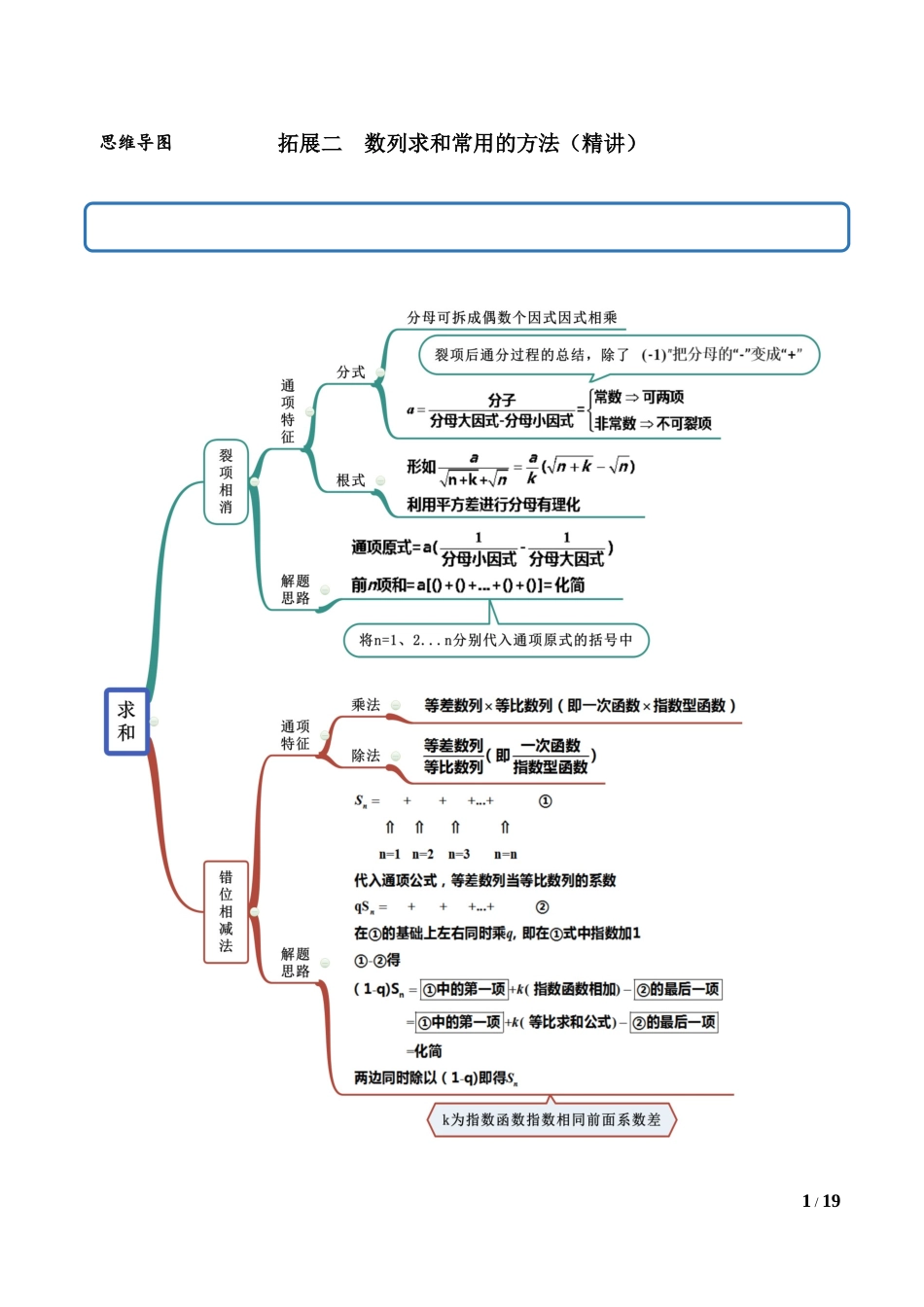
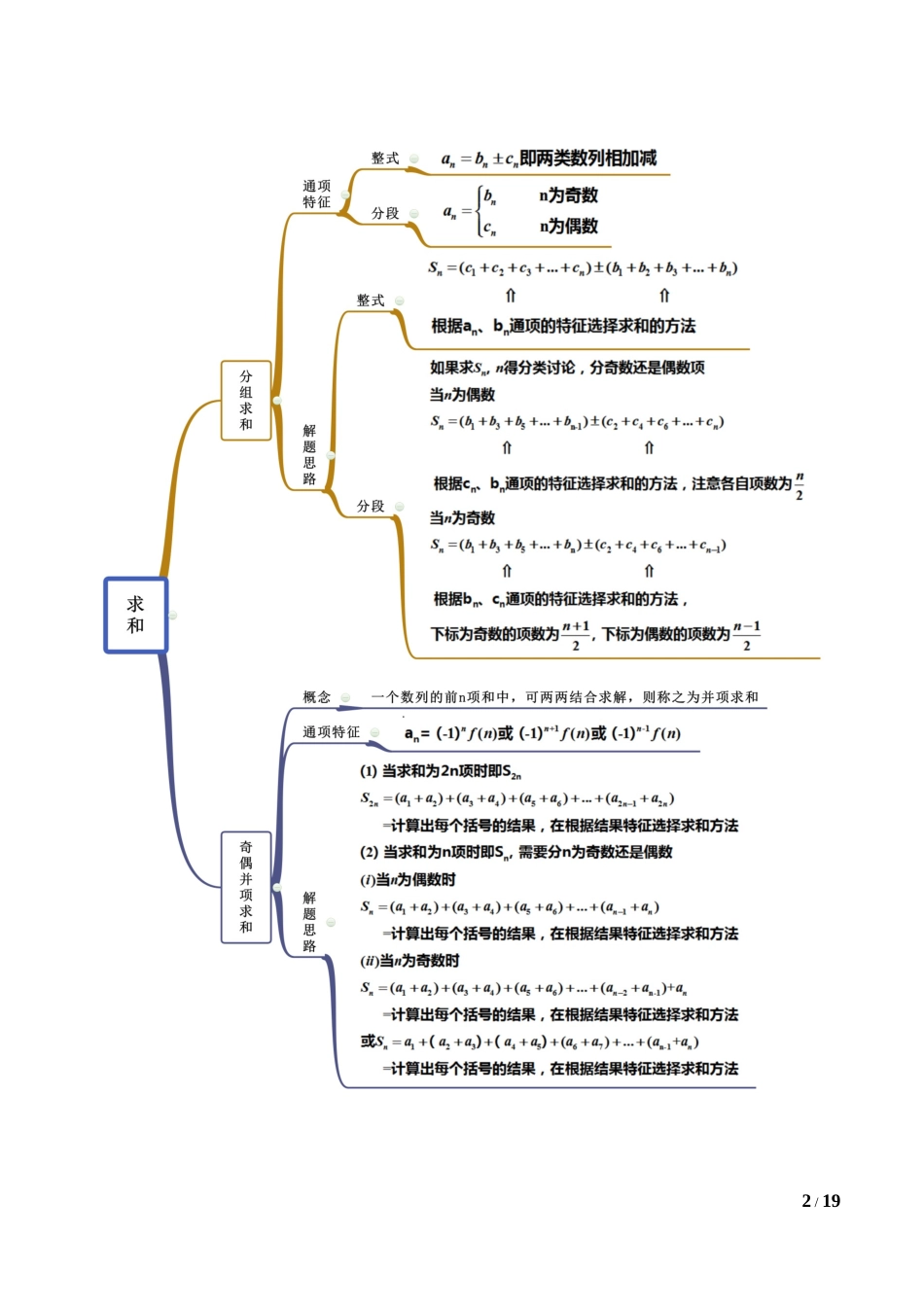
1/19拓展二数列求和常用的方法(精讲)思维导图2/193/19考点一裂项相消法【例1】(2021·全国高二课时练习)数列{an}的前n项和为Sn,an是Sn和1的等差中项,等差数列{bn}满足b1+S4=0,b9=a1.(1)求数列{an},{bn}的通项公式;(2)若cn=,求数列{cn}的前n项和Wn.【答案】(1)an=2n-1;bn=2n-17;(2).【解析】(1) an是Sn和1的等差中项,∴Sn=2an-1,当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,∴an=2an-1,当n=1时,a1=S1=2a1-1.∴a1=1且an≠0,∴=2,∴{an}是首项为1,公比为2的等比数列,∴an=2n-1,Sn=a1+a2+…+an==2n-1.设{bn}的公差为d,b1=-S4=-15,b9=-15+8d=1,∴d=2,∴bn=-15+(n-1)×2=2n-17.(2)cn==,常见考法4/19∴Wn===.【一隅三反】1.(2021·全国)已知等差数列{an}满足:a3=7,a5+a7=26,{an}的前n项和为Sn.(1)求an及Sn;(2)令bn=(n∈N*),求数列{bn}的前n项和Tn.【答案】(1)an=2n+1,Sn=n(n+2);(2).【解析】(1)设等差数列{an}的首项为a1,公差为d,由于a3=7,a5+a7=26,∴a1+2d=7,2a1+10d=26,解得a1=3,d=2.∴an=2n+1,Sn=n(n+2).(2) an=2n+1,∴-1=4n(n+1),∴.故Tn=b1+b2+…+bn∴数列{bn}的前n项和Tn=.2(2021·六盘山高级中学高二月考(文))已知数列的各项均为正数,其前项和满足.(1)证明:数列是等差数列;5/19(2)设数列,求数列的前项和.【答案】(1)证明见解析;(2).【解析】(1)由题意,数列的各项均为正数,且满足.当时,,可得,即,因为,所以,当时,,解得.所以数列是首项为1,公差为2的等差数列.所以数列是等差数列为.(2)由(1)知,可得,所以.3.(2021·内蒙古集宁一中(文))等差数列中,,且满足.(1)求数列的通项公式;(2)若,求数列的前项和.【答案】(1);(2).【解析】(1)由已知等差数列中,,由可得,由等差数列的定义可得:是以为首项,以为公差的等差数列,6/19所以.(2)由(1)得.所以.考点二错位相减法【例2】(2021·六盘山高级中学高二月考)设等差数列中,,各项均为正数的数列的前项为,已知点在函数的图像上,且.(1)求数列和的通项公式;(2)设数列满足,数列的前项和为.【答案】(1);;(2).【解析】(1)解:设等差数列的公差为,则,∴; 点在函数的图像上∴,∴,即;∴数列为等比数列,首项为,公比为3.∴,即...