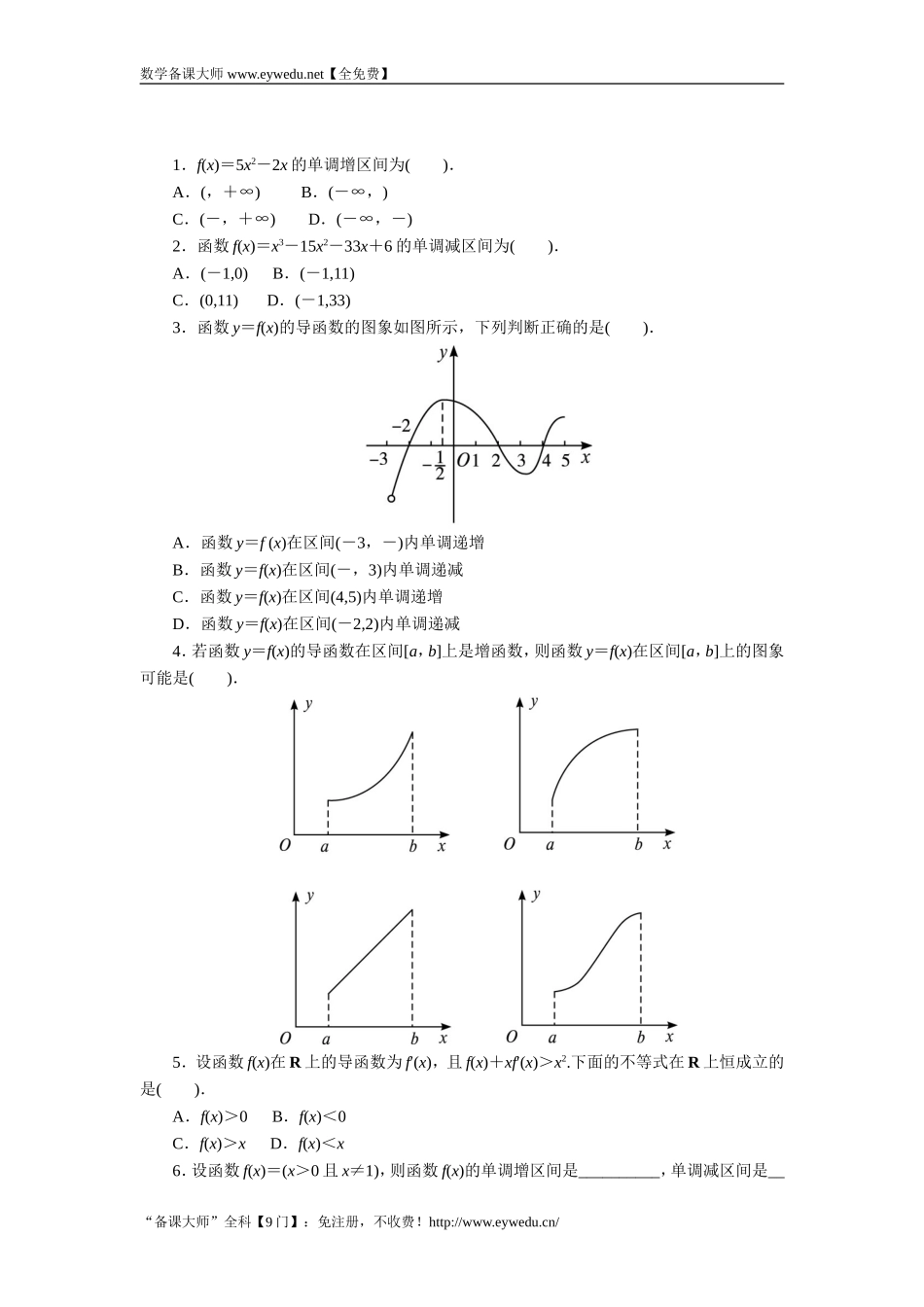
数学备课大师www.eywedu.net【全免费】1.f(x)=5x2-2x的单调增区间为().A.(,+∞)B.(-∞,)C.(-,+∞)D.(-∞,-)2.函数f(x)=x3-15x2-33x+6的单调减区间为().A.(-1,0)B.(-1,11)C.(0,11)D.(-1,33)3.函数y=f(x)的导函数的图象如图所示,下列判断正确的是().A.函数y=f(x)在区间(-3,-)内单调递增B.函数y=f(x)在区间(-,3)内单调递减C.函数y=f(x)在区间(4,5)内单调递增D.函数y=f(x)在区间(-2,2)内单调递减4.若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是().5.设函数f(x)在R上的导函数为f′(x),且f(x)+xf′(x)>x2.下面的不等式在R上恒成立的是().A.f(x)>0B.f(x)<0C.f(x)>xD.f(x)<x6.设函数f(x)=(x>0且x≠1),则函数f(x)的单调增区间是__________,单调减区间是__“备课大师”全科【9门】:免注册,不收费!http://www.eywedu.cn/数学备课大师www.eywedu.net【全免费】________.7.求下列函数的单调区间.(1)f(x)=x-x3;(2)f(x)=3x2-2lnx.8.已知函数f(x)=(a+1)lnx+ax2+1.(1)讨论函数f(x)的单调性;(2)设a≤-2,证明:对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|.“备课大师”全科【9门】:免注册,不收费!http://www.eywedu.cn/数学备课大师www.eywedu.net【全免费】参考答案1.Af′(x)=10x-2.令f′(x)>0,得x>,故选A.2.Bf′(x)=3x2-30x-33=3(x-11)(x+1).由(x-11)(x+1)<0,得单调减区间为(-1,11).3.C由图可知在区间(-2,2)和(4,5)内,f′(x)>0,故函数y=f(x)在区间(-2,2)和(4,5)内递增;在区间(-3,-2)和(2,4)内,f′(x)<0,故函数f(x)在区间(-3,-2)和(2,4)内单调递减,故选C.4.A因为函数y=f(x)的导函数y=f′(x)在区间[a,b]上是增函数,所以f(x)在区间[a,b]上各点处的斜率k是递增的,由图易知选A.注意选项C中,y′=k为常数.5.A由题意,f(x)+xf′(x)>x2≥0,∴G(x)=xf(x)在R上为增函数,且G(0)=0.于是有x>0时,G(x)=xf(x)>0,∴f(x)>0.当x<0时,G(x)=xf(x)<0,∴f(x)>0.∴f(x)>0在x∈R上恒成立.6.(0,)(,1)和(1,+∞)f′(x)=()′=.令f′(x)>0,即->0,得1+lnx<0,即x<.令f′(x)<0,即-<0,得1+lnx>0,即x>.又x>0且x≠1,∴函数的单调递增区间为(0,),单调递减区间为(,1)和(1,+∞).7.解:(1)f′(x)=1-3x2.令1-3x2>0,解得-<x<.因此,函数f(x...