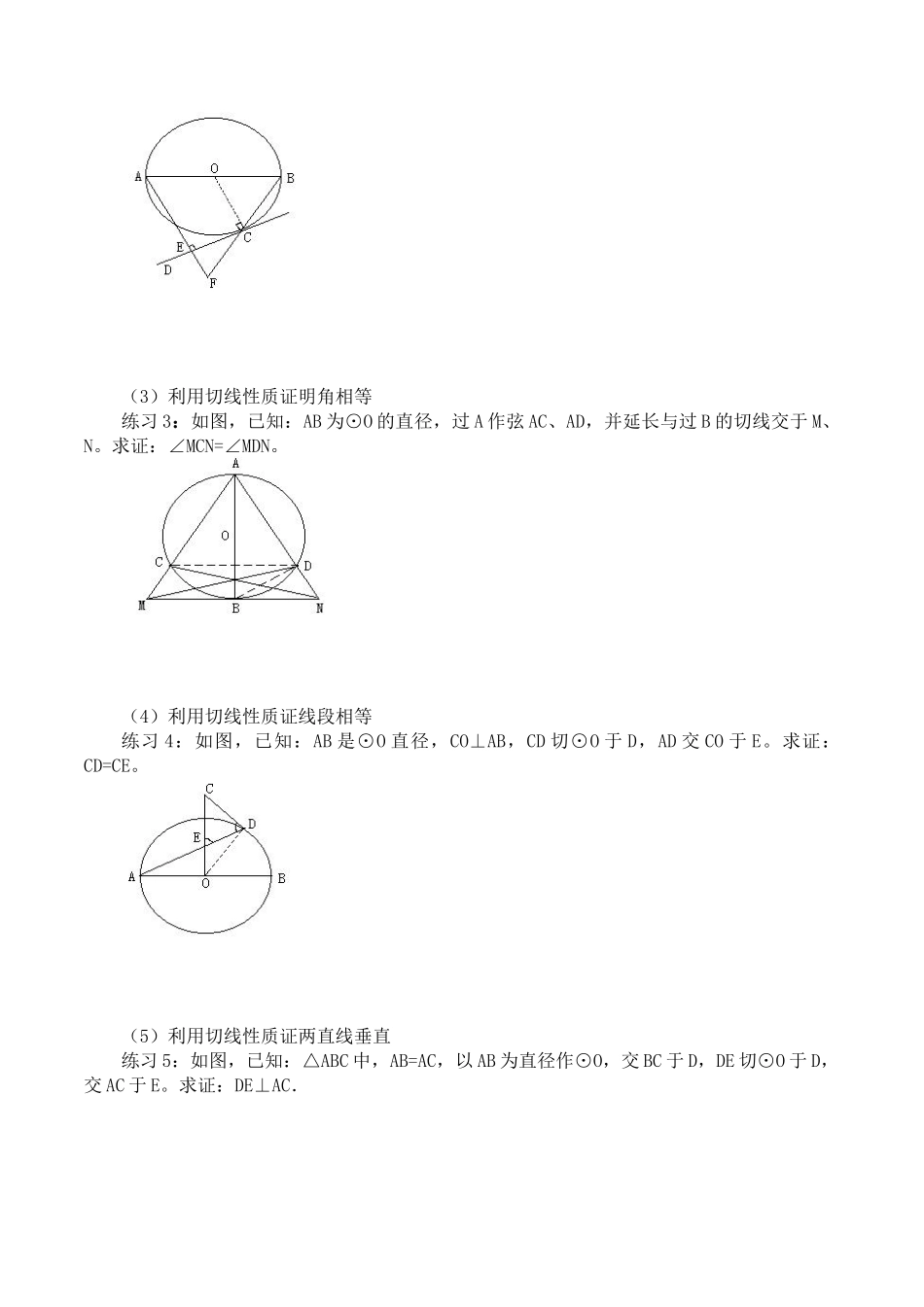
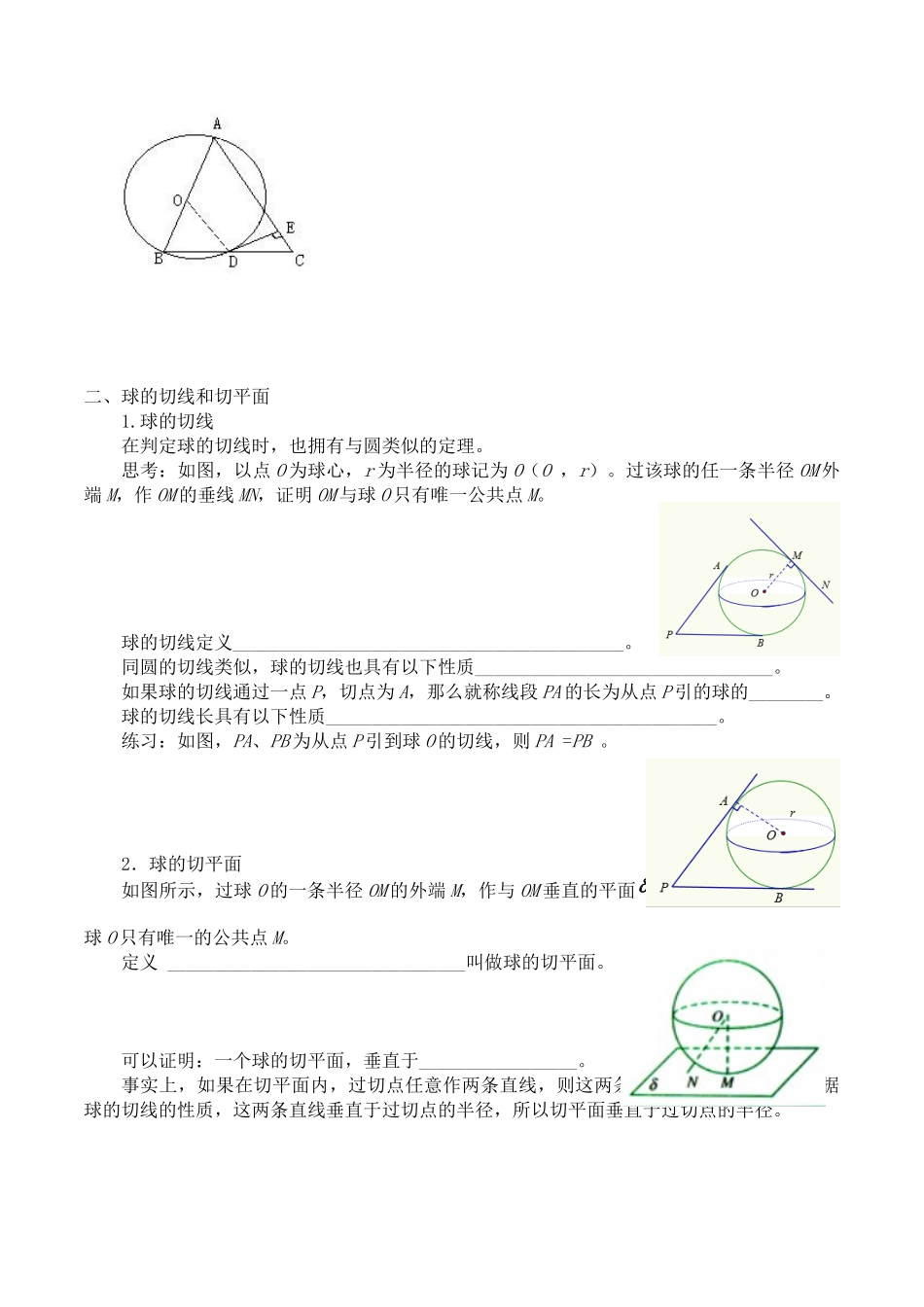
圆的切线【学习目标】1、理解切线的判定定理及性质定理;2、熟练运用切线的判定定理及性质定理解决一些实际问题。3.掌握球的切线、切平面的概念。【学习重难点】切线的判定定理及性质定理;球的切线切平面相关概念。【学习过程】一、圆的切线1.圆的切线性质定理是__________________________________________________。2.切线的性质有:(1)______________________________________;(2)______________________________________;(3)______________________________________;(4)______________________________________;(5)______________________________________。应用切线的性质能解决几何计算与证明中的有关问题。(1)利用切线性质计算线段的长度练习1:如图,已知:AB是⊙O的直径,P为延长线上的一点,PC切⊙O于C,CD⊥AB于D,又PC=4,⊙O的半径为3.求OD的长。(2)利用切线性质计算角的度数练习2:如图,已知:AB是⊙O的直径,CD切⊙O于C,AE⊥CD于E,BC的延长线与AE的延长线交于F,且AF=BF。求:∠A的度数。(3)利用切线性质证明角相等练习3:如图,已知:AB为⊙O的直径,过A作弦AC、AD,并延长与过B的切线交于M、N。求证:∠MCN=∠MDN。(4)利用切线性质证线段相等练习4:如图,已知:AB是⊙O直径,CO⊥AB,CD切⊙O于D,AD交CO于E。求证:CD=CE。(5)利用切线性质证两直线垂直练习5:如图,已知:△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,DE切⊙O于D,交AC于E。求证:DE⊥AC.二、球的切线和切平面1.球的切线在判定球的切线时,也拥有与圆类似的定理。思考:如图,以点O为球心,r为半径的球记为O(O,r)。过该球的任一条半径OM外端M,作OM的垂线MN,证明OM与球O只有唯一公共点M。球的切线定义__________________________________________。同圆的切线类似,球的切线也具有以下性质________________________________。如果球的切线通过一点P,切点为A,那么就称线段PA的长为从点P引的球的________。球的切线长具有以下性质__________________________________________。练习:如图,PA、PB为从点P引到球O的切线,则PA=PB。2.球的切平面如图所示,过球O的一条半径OM的外端M,作与OM垂直的平面,则容易证明平面与球O只有唯一的公共点M。定义________________________________叫做球的切平面。可以证明:一个球的切平面,垂直于_________________。事实上,如果在切平面内,过切点任意作两条直线,则这两条直线都是球的切线。根据球的切线的性质,这两条直线垂直于过切点的半径,所以切平面垂直于过切点的半径。