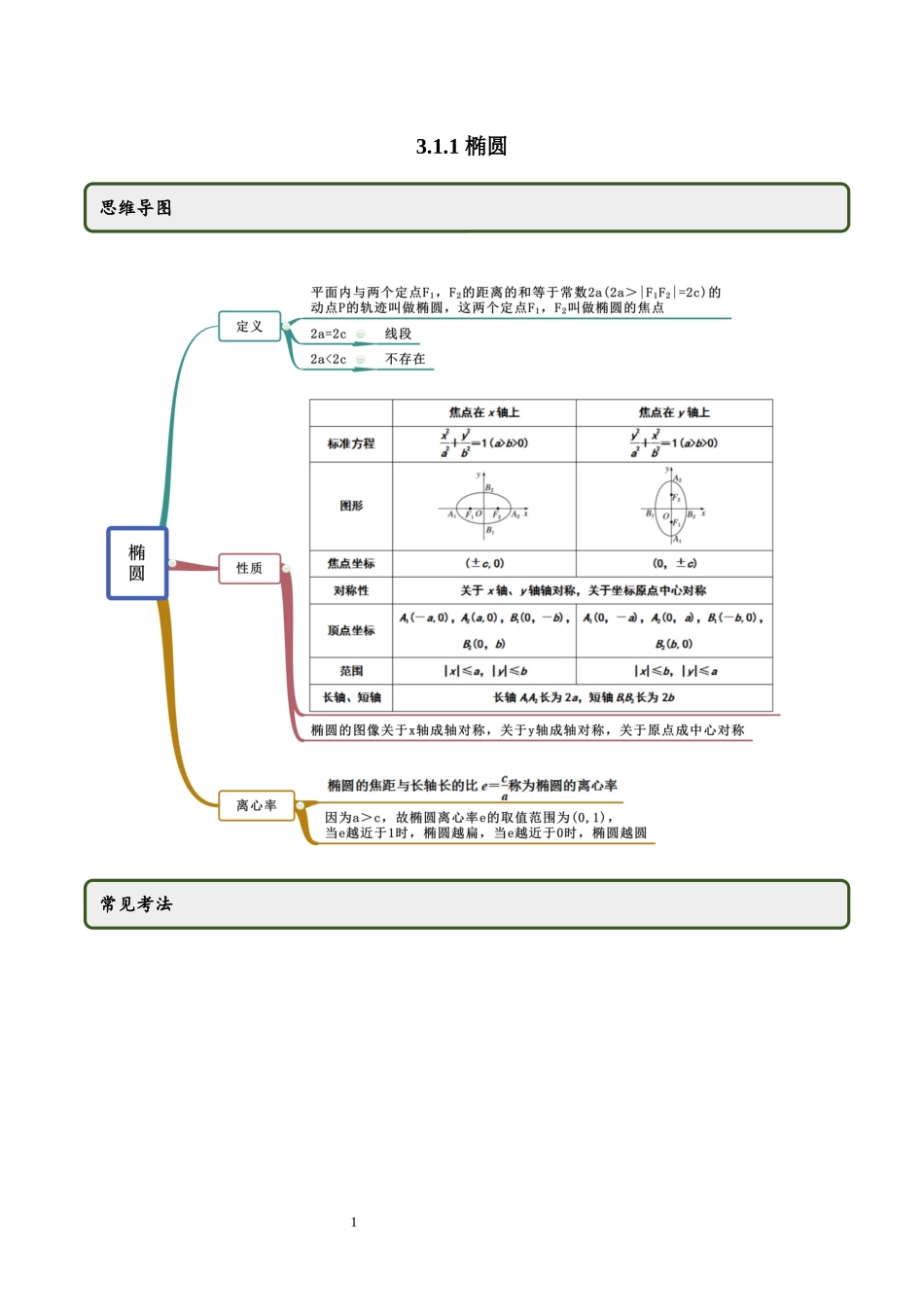
13.1.1椭圆思维导图常见考法2考点一椭圆的定义【例1】(1)(2020·上海徐汇.高二期末)已知、是定点,.若动点满足,则动点的轨迹是()A.直线B.线段C.圆D.椭圆(2)(2019·宁波市第四中学高二期中)设是椭圆上的点.若是椭圆的两个焦点,则等于()A.4B.5C.8D.10【一隅三反】1.(2020·河南省鲁山县第一高级中学高二月考)若椭圆上一点P到左焦点的距离为5,则其到右焦点的距离为()A.5B.3C.2D.1椭圆是在平面内定义的,所以“平面内”这一条件不能忽视.定义中到两定点的距离之和是常数,而不能是变量.常数(2a)必须大于两定点间的距离,否则轨迹不是椭圆,这是判断曲线是否为椭圆的限制条件.32.(2020·东城.北京五十五中高二月考)若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为()A.4B.194C.94D.143.下列命题是真命题的是________.(将所有真命题的序号都填上)①已知定点F1(-1,0),F2(1,0),则满足|PF1|+|PF2|=的点P的轨迹为椭圆;②已知定点F1(-2,0),F2(2,0),则满足|PF1|+|PF2|=4的点P的轨迹为线段;③到定点F1(-3,0),F2(3,0)的距离相等的点的轨迹为椭圆.考点二椭圆定义的运用【例2-1】(1)(2019·福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是()A.B.C.D.(2)(2019·江苏省苏州实验中学高二期中)方程表示椭圆,则实数的取值范围()A.B.C.D.且把方程写成椭圆的标准方程形式,得到形式,要想表示(1)焦点在轴上的椭圆,必须要满足,解这个不等式就可求出实数的取值范围.(2)焦点在x轴上的椭圆,必须要满足A>B>0,解这个不等式就可求出实数的取值范围.(3)椭圆,必须要满足解这个不等式就可求出实数的取值范围4【一隅三反】1.(2020·广东高三月考(文))“”是“方程表示椭圆”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.(2017·浙江东阳.高二期中)如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是()A.B.C.或D.或3.(2019·北京北师大实验中学高二期中)若方程表示焦点在轴上的椭圆,则的取值范围是()A.B.C.D.【例2-2】(1)(2018·黑龙江哈尔滨三中高二期中(文))已知的顶点,在椭圆上,顶点是椭圆的一个焦点,且椭圆的另一个焦点在上,则的周长是()A.B.C.D.(2)(2019·广西田阳高中))已知是椭圆上一点,为椭圆的两焦点,且,则面积为()5A.B.C.D.【一隅三反】1.(2019·黑...