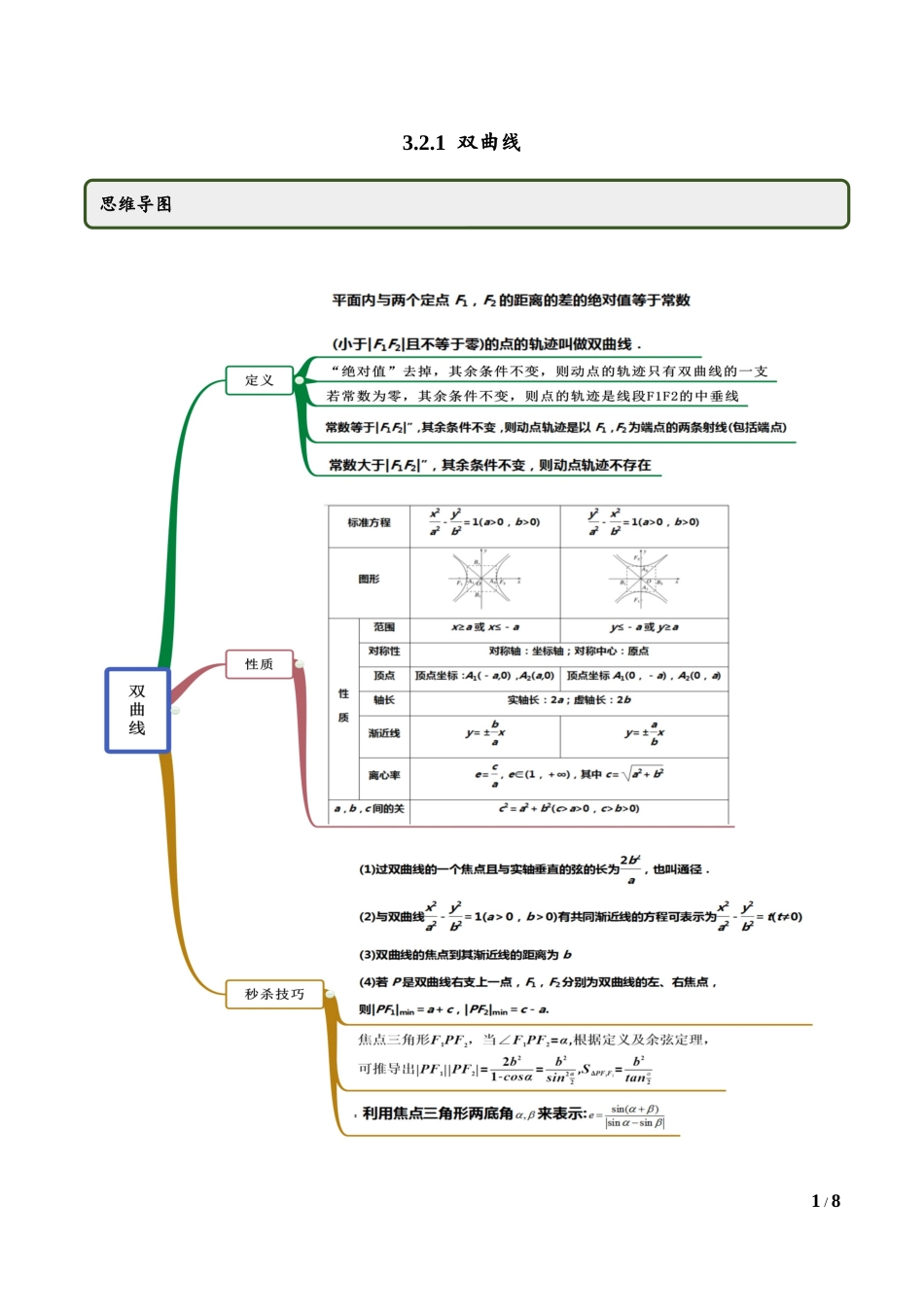
1/83.2.1双曲线思维导图2/8考点一双曲线的定义【例1】(1)(2020·日喀则市拉孜高级中学高二期末(文))到两定点的距离之差的绝对值等于6的点的轨迹为()A.椭圆B.两条射线C.双曲线D.线段(2)(2020·甘肃省民乐县第一中学高三其他(理))已知双曲线的上、下焦点分别为,,点P在双曲线C上,若,则()A.38B.24C.38或10D.24或4【一隅三反】1.(2020·广东濠江.金山中学高三三模(文))已知,则动点的轨迹是()A.一条射线B.双曲线右支C.双曲线D.双曲线左支2(2020·浙江杭州.高二期末)已知平面中的两点,则满足的点M的轨迹是()常见考法3/8A.椭圆B.双曲线C.一条线段D.两条射线3.(2020·浙江瓯海.温州中学高二期末)双曲线的左右焦点分别为,,点在双曲线上,若,则()A.B.C.或D.考点二双曲线定义的运用【例2】(1)(2020·江西高二期末(文))已知双曲线,直线l过其左焦点,交双曲线左支于A、B两点,且,为双曲线的右焦点,的周长为20,则m的值为()A.8B.9C.16D.20(2)(2020·四川南充.高二期末(理))设分别是双曲线的两个焦点,P是该双曲线上的一点,且,则的面积等于A.B.C.D.4/8【一隅三反】1.(2020·宁夏兴庆.银川九中)已知是双曲线的两个焦点,点为该双曲线上一点,若,且,则()A.1B.C.D.32.(2020·武威第八中学高二期末(理))已知双曲线:的左右焦点分别为,为的右支上一点,且,则的面积等于A.B.C.D.3.(2020·吉林松原)已知点是双曲线上一点,,分别为双曲线的左、右焦点,若的外接圆半径为4,且为锐角,则()A.15B.16C.18D.20求双曲线中焦点三角形面积的方法(1)方法一:①根据双曲线的定义求出||PF1|-|PF2||=2a;②利用余弦定理表示出|PF1|,|PF2|,|F1F2|之间满足的关系式;③通过配方,利用整体的思想求出|PF1|·|PF2|的值;④利用公式=×|PF1|·|PF2|sin∠F1PF2求得面积.(2)方法二:利用公式=×|F1F2|×|yP|(yP为P点的纵坐标)求得面积.5/8【例2-2】(2020·安徽贵池。池州一中高二期末(理))方程表示双曲线的充分不必要条件是()A.或B.C.D.或【一隅三反】1.(2020·全国高二课时练习)若m为实数,则“”是“曲线C:表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(2020·辽宁高三其他(理))若,则是方程表示双曲线的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(2020...