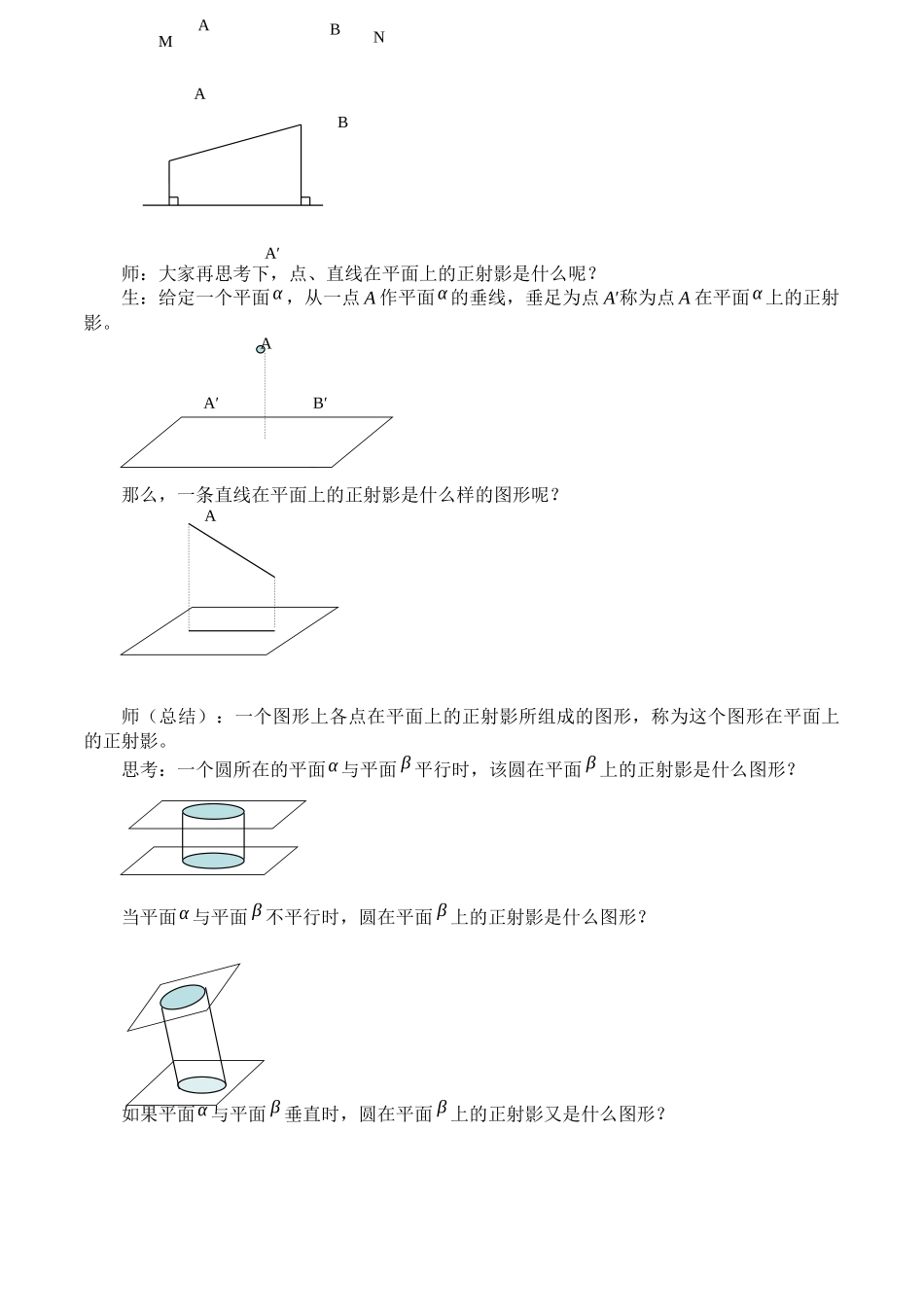
平行投影【教学目标】了解平行投影的含义和基本性质;正投影变换的性质。【教学重难点】重点:平行投影基本定理和性质。难点:平行投影定理和正投影变换性质的证明。【教学过程】新课讲授师:什么是平行投影呢?生:设空间有一个点集M,一个平面a和一条不平行于平面a的直线s,经过M中每一点X,作平行于s或与s重合的直线交平面a于点Y,这样就确定了一个由M到a的映射Y=s(x),称此映射为由s确定的点集M到平面a的平行投影。师:那平行投影的定理是什么呢?生:不平行于投影线的线段,在平面上的投影仍为线段,线段上的点分线段的比保持不变,端点仍为端点。师:很好。那我们一起看看课本上是如何证明这个定理的。师:平面p到平面a的一对一的映射,称为平面p到平面a的平行投影变换。师:平行投影变换的基本性质有哪些呢?1.线段的投影仍为线段;2.线段中心的投影为投影的中点;3.平行四边形的投影仍为平行四边形;4.平行线段的投影仍为平行线段;5.平行或共线线段的比等于线段投影的比;6.若原平面和像平面平行,则线段和它的投影长度相等;7.若两平面相交,则平行于基线的线段和它的投影长度相等。8.两个多边形的面积比,等于其投影的面积比。师:看看下面的例子,思考什么是正投影呢?1.点在直线上的正射影2.直线在直线上的正射影A‘ANM师:大家再思考下,点、直线在平面上的正射影是什么呢?生:给定一个平面α,从一点A作平面α的垂线,垂足为点A′称为点A在平面α上的正射影。那么,一条直线在平面上的正射影是什么样的图形呢?师(总结):一个图形上各点在平面上的正射影所组成的图形,称为这个图形在平面上的正射影。思考:一个圆所在的平面α与平面β平行时,该圆在平面β上的正射影是什么图形?当平面α与平面β不平行时,圆在平面β上的正射影是什么图形?如果平面α与平面β垂直时,圆在平面β上的正射影又是什么图形?BB′A′AA′ABABAMN显然,正射影是平行射影的特例。思考:两条相交直线的平行射影是否还是相交直线?两条平行直线的平行射影是否还是平行直线?将一个放在桌面上的玻璃杯中倒入半杯水,观察水平面所成的图形;如果将玻璃杯倾斜一定的角度,此时水平面又是一个什么样的图形?可以看出水平面是一个椭圆。师:正投影变换的性质是什么呢?生:若正投影变换的原平面和像平面相交,则垂直于基线的直线的像仍垂直于基线。师:那我们再一起看看课本上是如何证明这个性质的。课堂小结:回顾本课学习了哪些知识?