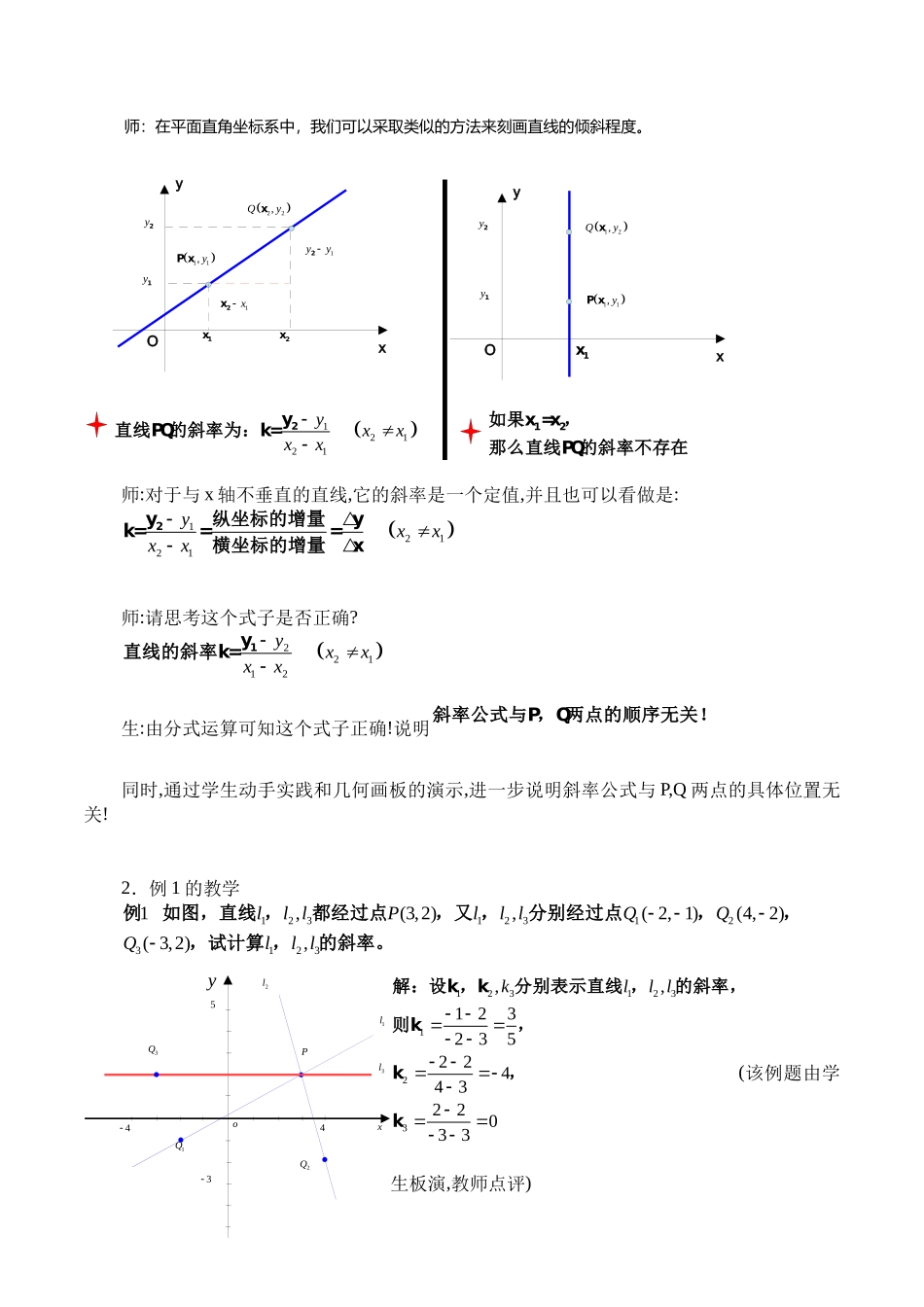
直线的斜率【教材分析】直线的斜率是在研究图形的基础上,又一种新的研究图形性质方法——解析法,解析法是以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算研究几何图形的性质方法是解析几何中最基本的研究方法,本节课体现了这种方法的具体特征,是实现向解析法过渡的最好案例,它为今后如何用解析法研究几何问题奠定了基础本节课在两点确定一条直线的基础上探讨了。确定直线的另一种方法,即利用直线上一点和倾斜角能确定一条直线,并利用代数方法表示了确定直线几何要素——倾斜角和斜率,然后进一步利用倾斜角和斜率研究直线的位置状态以及直线间的关系。1.本节课是在学生学习了函数,对一些基本初等函数的图象和性质已掌握的前提下,解析几何的第一节课,教师应向学生展示在平面直角坐标系下,数和形的关系,从而揭示解析几何的研究方法和解决的问题,为今后的学习奠定基础。2.建议在过程中从学生熟悉的一次函数的图象着手,导出解析几何这门学科,从解析几何的研究方法和平面内确定一条直线的条件,启发学生探索和发现刻画直线倾斜程度的量。3.本节课的重点是直线的斜率,由两点确定一条直线联想能否用两点的坐标来表示,结合学生熟悉的坡度的定义,揭示如何用两点的坐标表示,以及表示的合理性对直线斜率公式的应。用,要注意公式成立的条件和公式的正用逆用、,特别要说明斜率不存在时,直线存在(让学生体验此时直线的位置,以加深印象),在逆用时强调斜率是一比值,由它能知道直线在坐标系中的位置(体现数和形的结合,让学生利用图象发现并归纳),若再有一点即知直线上另一点的坐标(启发学生利用斜率公式进行求解,提醒注意不唯一)。【教学目标】1.知识与技能(1)理解直线的斜率的概念。(2)掌握过两点的直线的斜率公式。(3)理解直线斜率的存在条件。2.过程与方法通过分析“坡度”这一学生熟悉的概念,得到研究直线倾斜程度的量——斜率通过师生。探讨,得出直线的斜率公式,并以此为基础理解直线斜率的存在性;学生通过实践,运用所学知识解决有关问题。3.情感态度与价值观通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合思想,培养学生树立辩证统一的观点;培养学生形成严谨的科学态度和求实的数学精神。【教学重难点】(1)重点:直线的斜率的概念;斜率公式的推导与运用。(2)难点:直线斜率的存在性;斜率的符号与直线倾斜方向的关系。【教学准备】计算机投影、。【教学方法】启发引导合作探究讨论点评、、。【教学过程】一新课导入、:师:这...