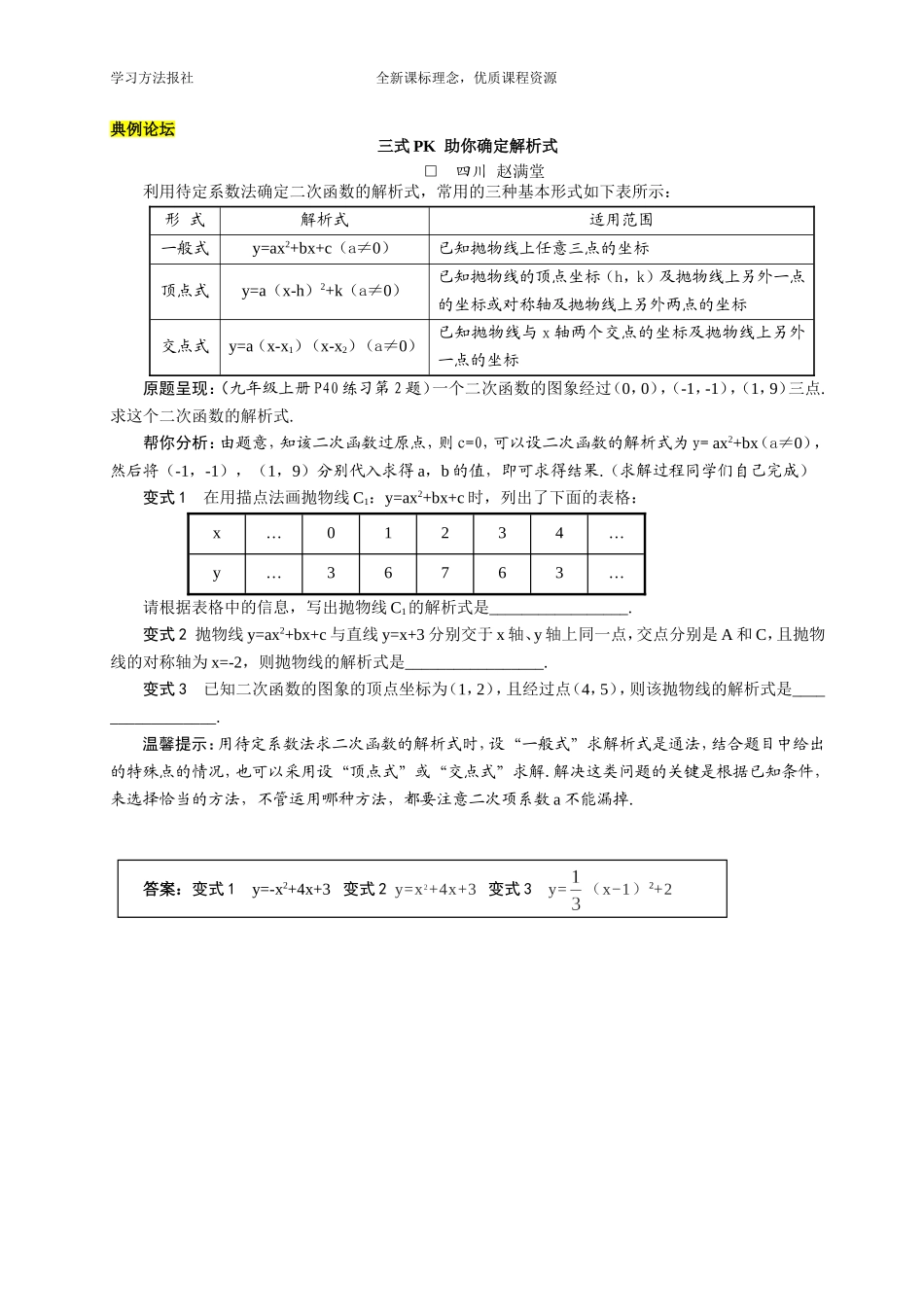
学习方法报社全新课标理念,优质课程资源典例论坛三式PK助你确定解析式□四川赵满堂利用待定系数法确定二次函数的解析式,常用的三种基本形式如下表所示:形式解析式适用范围一般式y=ax2+bx+c(a≠0)已知抛物线上任意三点的坐标顶点式y=a(x-h)2+k(a≠0)已知抛物线的顶点坐标(h,k)及抛物线上另外一点的坐标或对称轴及抛物线上另外两点的坐标交点式y=a(x-x1)(x-x2)(a≠0)已知抛物线与x轴两个交点的坐标及抛物线上另外一点的坐标原题呈现:(九年级上册P40练习第2题)一个二次函数的图象经过(0,0),(-1,-1),(1,9)三点.求这个二次函数的解析式.帮你分析:由题意,知该二次函数过原点,则c=0,可以设二次函数的解析式为y=ax2+bx(a≠0),然后将(-1,-1),(1,9)分别代入求得a,b的值,即可求得结果.(求解过程同学们自己完成)变式1在用描点法画抛物线C1:y=ax2+bx+c时,列出了下面的表格:x…01234…y…36763…请根据表格中的信息,写出抛物线C1的解析式是_________________.变式2抛物线y=ax2+bx+c与直线y=x+3分别交于x轴、y轴上同一点,交点分别是A和C,且抛物线的对称轴为x=-2,则抛物线的解析式是_________________.变式3已知二次函数的图象的顶点坐标为(1,2),且经过点(4,5),则该抛物线的解析式是_________________.温馨提示:用待定系数法求二次函数的解析式时,设“一般式”求解析式是通法,结合题目中给出的特殊点的情况,也可以采用设“顶点式”或“交点式”求解.解决这类问题的关键是根据已知条件,来选择恰当的方法,不管运用哪种方法,都要注意二次项系数a不能漏掉.答案:变式1y=-x2+4x+3变式2y=x2+4x+3变式3y=(x−1)2+2