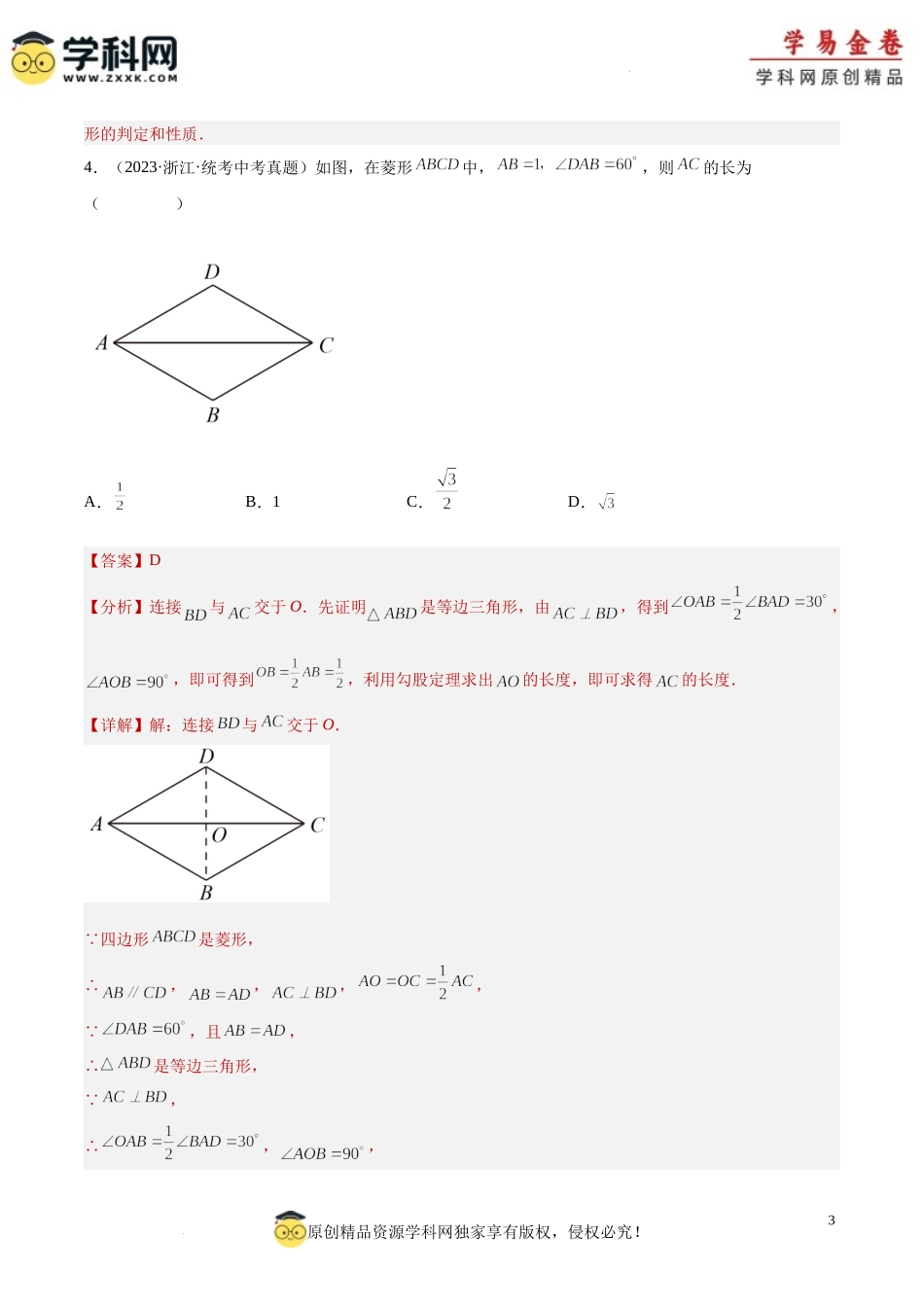
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司专题18矩形菱形正方形(39题)一、单选题1.(2023·湖南·统考中考真题)如图,菱形中,连接,若,则的度数为()A.B.C.D.【答案】C【分析】根据菱形的性质可得,则,进而即可求解.【详解】解: 四边形是菱形∴,∴, ,∴,故选:C.【点睛】本题考查了菱形的性质,熟练掌握是菱形的性质解题的关键.2.(2023·湖南常德·统考中考真题)如图1,在正方形中,对角线相交于点O,E,F分别为,上的一点,且,连接.若,则的度数为()2原创精品资源学科网独家享有版权,侵权必究!A.B.C.D.【答案】C【分析】首先根据正方形的性质得到,,然后结合得到,然后证明出,最后利用三角形内角和定理求解即可.【详解】 四边形是正方形∴, ∴,∴∴又 ,∴∴∴∴故选:C.【点睛】此题考查了正方形的性质,全等三角形的性质和判定,等腰直角三角形三角形的性质等知识,解题的关键是熟练掌握以上知识点.3.(2023·湖南常德·统考中考真题)下列命题正确的是()A.正方形的对角线相等且互相平分B.对角互补的四边形是平行四边形C.矩形的对角线互相垂直D.一组邻边相等的四边形是菱形【答案】A【分析】根据正方形、平行四边形、矩形、菱形的各自性质和构成条件进行判断即可.【详解】A、正方形的对角线相等且互相垂直平分,描述正确;B、对角互补的四边形不一定是平行四边形,只是内接于圆,描述错误;C、矩形的对角线不一定垂直,但相等,描述错误;D、一组邻边相等的平行四边形才构成菱形,描述错误.故选:A.【点睛】本题考查平行四边形、矩形、菱形、正方形的性质和判定,解题的关键是熟悉掌握各类特殊四边3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司形的判定和性质.4.(2023·浙江·统考中考真题)如图,在菱形中,,则的长为()A.B.1C.D.【答案】D【分析】连接与交于O.先证明是等边三角形,由,得到,,即可得到,利用勾股定理求出的长度,即可求得的长度.【详解】解:连接与交于O. 四边形是菱形,∴,,,, ,且,∴是等边三角形, ,∴,,4原创精品资源学科网独家享有版权,侵权必究!∴,∴,∴,故选:D.【点睛】此题主要考查了菱形的性质、勾股定理、等边三角形的判定和性质、角所对直角边等于斜边的一半,关键是熟练掌握菱形的性质.5.(2023·上海·统考中考真题)在四边形中,.下列说法能使四边形为矩形的是...