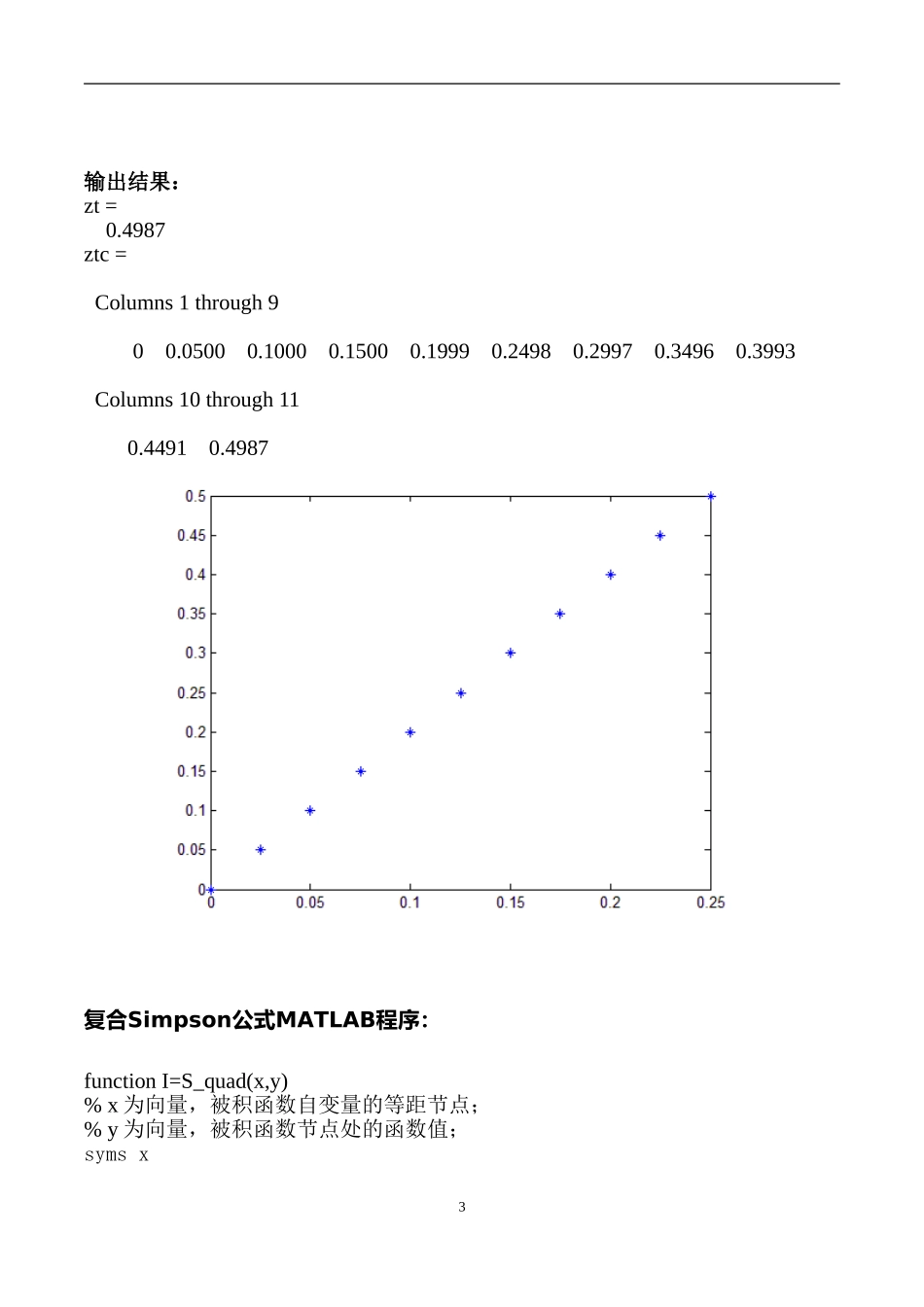
数值分析实验---数值积分实验名称:数值积分的复合梯形公式,Simpson公式,Romberg公式的算法姓名:包昂专业:材料加工学号:2013230052课题九数值积分与数值微分一、问题提出计算下列积分值:(1)(2)(3)1(4)要求:1、编制数值积分算法的程序;2、分别用两种算法计算同一个积分,并比较其结果;3、分别取不同步长,试比较计算结果(如n=10,20等);4、给定精度要求ε,试用变步长算法,确定最佳步长。二、问题分析由上可知这几个积分找不到用初等函数表示的原函数,直接计算起来很困难,因此我们考虑利用函数在若干点得函数值,近似地计算该函数在一个区间上得定积分。这里采用的方法有三种:复合梯形公式,复合Simpson公式,Romberg算法。三、实验程序及注释(1)复合梯形公式MATLAB程序:functionI=T_quad(x,y)%复化梯形求积公式,其中,%x为向量,被积函数自变量的等距节点;%y为向量,被积函数节点处的函数值;h=1/40;x=0:h:1/4;y=(4-(sin(x)).^2).^(1/2);zt=trapz(x,y),ztc=cumtrapz(x,y),plot(x,ztc,'*')2输出结果:zt=0.4987ztc=Columns1through900.05000.10000.15000.19990.24980.29970.34960.3993Columns10through110.44910.4987复合Simpson公式MATLAB程序:functionI=S_quad(x,y)%x为向量,被积函数自变量的等距节点;%y为向量,被积函数节点处的函数值;symsx3L=inline('(4-(sin(x)).^2).^(1/2)');[QS,FCNTS]=quad(L,0,1/4,1.e-4,2)输出结果:90.00000000006.78950000e-0020.1357639381110.06789500001.14210000e-0010.2279455207130.18210500006.78950000e-0020.1350016588QS=0.4987FCNTS=13(2)复合梯形公式MATLAB程序:functionI=T_quad(x,y)%复化梯形求积公式,其中,%x为向量,被积函数自变量的等距节点;%y为向量,被积函数节点处的函数值;h=1/10;x=0.1:h:1;y=(sin(x))./x;zt=trapz(x,y),ztc=cumtrapz(x,y),plot(x,ztc,'*')输出结果:zt=40.8459ztc=Columns1through900.09960.19850.29640.39310.48810.58110.67200.7603Column100.8459复合Simpson公式MATLAB程序:functionI=S_quad(x,y)%x为向量,被积函数自变量的等距节点;%y为向量,被积函数节点处的函数值;symsxL=inline('(sin(x))./x');[QS,FCNTS]=quad(L,0,1,1.e-4,2)输出结果:100.00000000002.71580000e-0010.27046964965120.27158000004.56840000e-0010.4368170437140.72842000002.71580000e-0010.2387963767QS=0.9461FCNTS=14(3)复合梯形公式MATLAB程序:fu...