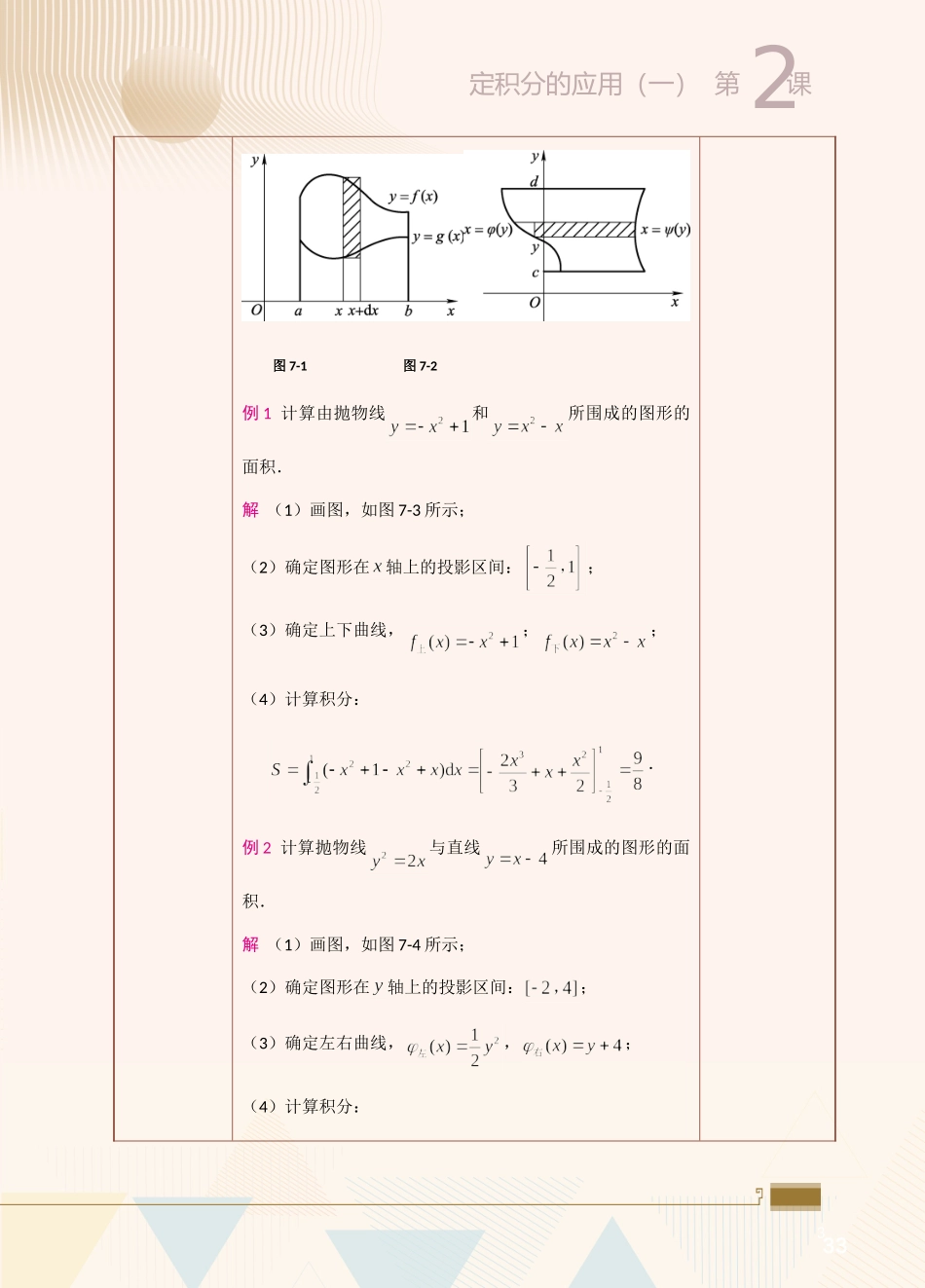
27定积分的应用(一)第课课题定积分的应用(一)——定积分的微元法、定积分的几何应用课时2课时(90min)教学目标知识技能目标:(1)理解定积分的微元法。(2)了解定积分在几何上的应用。思政育人目标:借助直观的几何图形讲解微元法,并介绍定积分在几何领域的应用,使学生体会到数学在实际问题中的应用,增加学生的学习兴趣;培养学生的逻辑思维、辩证思维和创新思维能力;引导学生运用所学知识揭示生活中的奥秘,在实践中深化认识,达到学以致用的目的。教学重难点教学重点:定积分的微元法教学难点:定积分在几何上的应用教学方法讲授法、问答法、讨论法、演示法、实践法教学用具电脑、投影仪、多媒体课件、教材教学设计第1节课:考勤(2min)→知识讲解(28min)→问题讨论(5min)→课堂测验(10min)第2节课:知识讲解(20min)→问题讨论(10min)→课堂测验(10min)→课堂小结(5min)教学过程主要教学内容及步骤设计意图第一节课考勤(2min)【教师】清点上课人数,记录好考勤【学生】班干部报请假人员及原因培养学生的组织纪律性,掌握学生的出勤情况知识讲解(28min)【教师】讲解定积分的微元法引入定积分概念时,从讨论曲边梯形的面积问题中知道,积分是以为底、以曲线为曲边的曲边梯形的面积.而微分表示点处以为宽的小曲边梯形面积的近似值,称为曲边学习定积分的微元法,掌握利用定积分求平面图形面积和立体体积的方法。边做边讲,及时巩固练习,实现教学做一27第课定积分的应用(一)2梯形的面积元素.那么,以为底的曲边梯形的面积A就是以面积元素为被积表达式,以为积分区间的定积分.一般情况下,为求某一量U(与变量有关的量),先确定变量的变化区间,再求量U的元素.若,则量U就是以为被积表达式,以为积分区间的定积分,即.这一方法通常称为微元法(或称为元素法).【教师】讲解利用定积分求平面图形的面积,并通过例题介绍其应用1.直角坐标情形设平面图形由上下两条曲线与及左右两条直线与所围成(见图7-1),则面积元素为,于是平面图形的面积为.类似地,由左右两条曲线与及上下两条直线与所围成的平面图形(见图7-2)的面积为.体化定积分的应用(一)第课273图7-1图7-2例1计算由抛物线和所围成的图形的面积.解(1)画图,如图7-3所示;(2)确定图形在轴上的投影区间:;(3)确定上下曲线,;;(4)计算积分:.例2计算抛物线与直线所围成的图形的面积.解(1)画图,如图7-4所示;(2)确定图形...