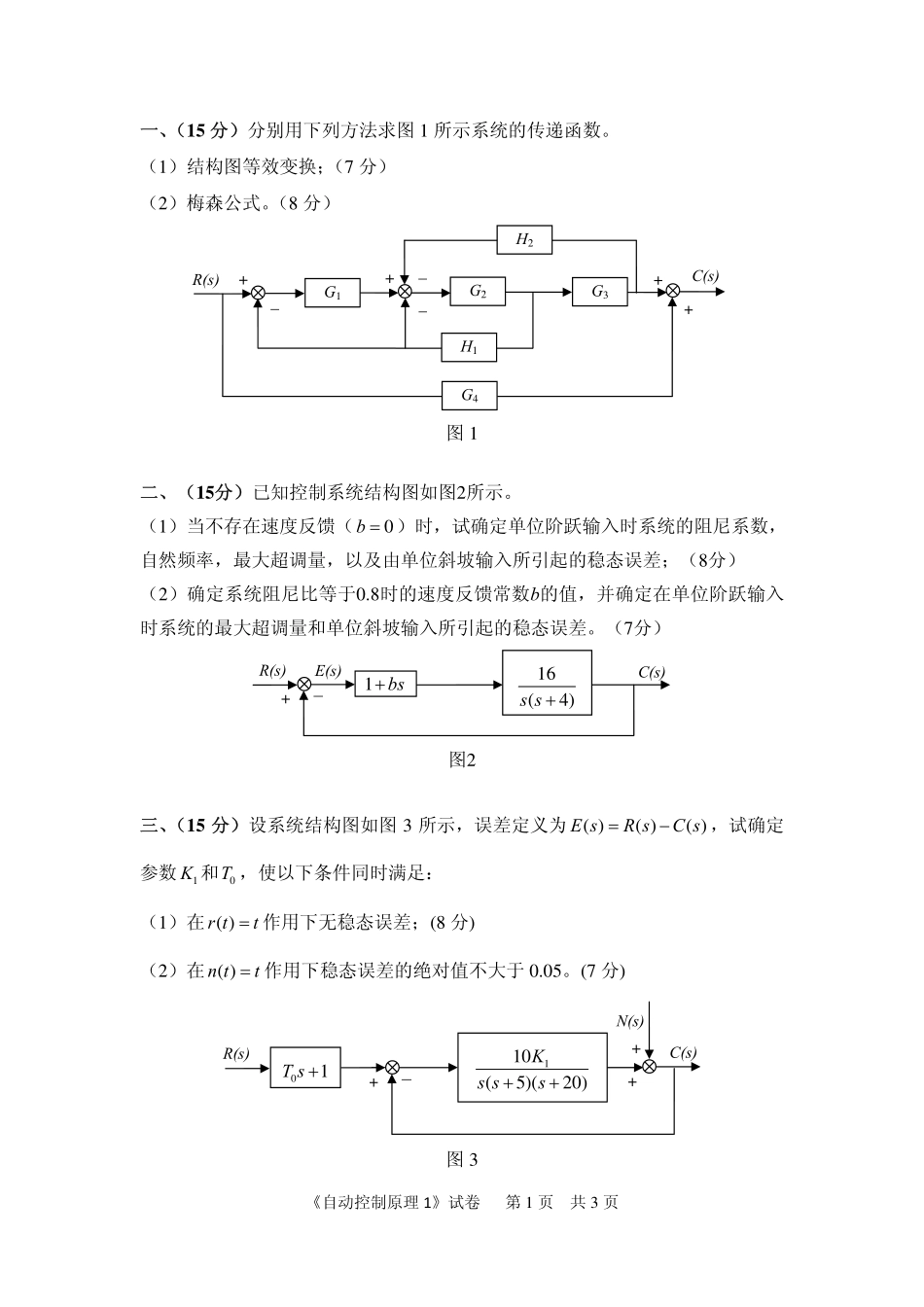
《自动控制原理1》试卷第1页共3页一、(15分)分别用下列方法求图1所示系统的传递函数。(1)结构图等效变换;(7分)(2)梅森公式。(8分)图1二、(15分)已知控制系统结构图如图2所示。(1)当不存在速度反馈(0b=)时,试确定单位阶跃输入时系统的阻尼系数,自然频率,最大超调量,以及由单位斜坡输入所引起的稳态误差;(8分)(2)确定系统阻尼比等于0.8时的速度反馈常数b的值,并确定在单位阶跃输入时系统的最大超调量和单位斜坡输入所引起的稳态误差。(7分)图2三、(15分)设系统结构图如图3所示,误差定义为()()()EsRsCs=−,试确定参数1K和0T,使以下条件同时满足:(1)在()rtt=作用下无稳态误差;(8分)(2)在()ntt=作用下稳态误差的绝对值不大于0.05。(7分)图3++R(s)-C(s)110(5)(20)Ksss++01Ts++N(s)+++C(s)G1G2G3H2H1G4R(s)---+-+E(s)C(s)R(s)16(4)ss+1bs+《自动控制原理1》试卷第2页共3页四、(15分)设单位负反馈控制系统的开环传递函数为:)7)(2()()(++=sssKsHsG(1)绘制系统的根轨迹图;(8分)(2)确定系统稳定时K的最大值;(4分)(3)确定阻尼比ξ=0.707时的K值。(3分)五、(15分)设系统的开环传递函数为:()(1)(0.21)KGssss=−+,其中10K=。(1)绘制该系统的奈氏图;(10分)(2)应用奈氏稳定判据判断其闭环系统的稳定性。(5分)六、(15分)绘制开环传递函数())17)(13)(1(+++=sssKsG的伯德图;若增益交界频率为3cω=,求系统的增益K。七、(20分)已知采样系统结构如图4所示,其中1TseZOHs−−=,采样周期1Ts=,221()(1)()ekekek=−+,(1)求()Dz;(5分)(2)求脉冲传递函数;(5分)(3)试确定系统稳定时的k值范围。(10分)图4八、(20分)建立一个合理的系统模型是进行系统分析和设计的基础。已知一单输入单输出线性定常系统的微分方程为:()4()3()()6()8()ytytytututut++=++������(1)给出状态空间模型(可控标准型),并画出对应的状态变量图;(15分)(2)归纳总结上述的实现过程,试简述由一个系统的n阶微分方程建立系统状态空间模型的思路。(5分)+—e1*(t)r(t)c(t)1ks+()DzZOHe2*(t)SS《自动控制原理1》试卷第3页共3页九、(20分)双足直立机器人可以近似为一个倒立摆装置,假设倒立摆系统的一个平衡点线性化状态空间模型如下:[]0100000101,100000010001101xxuyx⎡⎤⎡⎤⎢⎥⎢⎥−⎢⎥⎢⎥=+=⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦�其中,状态变量Txyyθθ⎡⎤=⎣⎦��,y是小车的位移,θ...