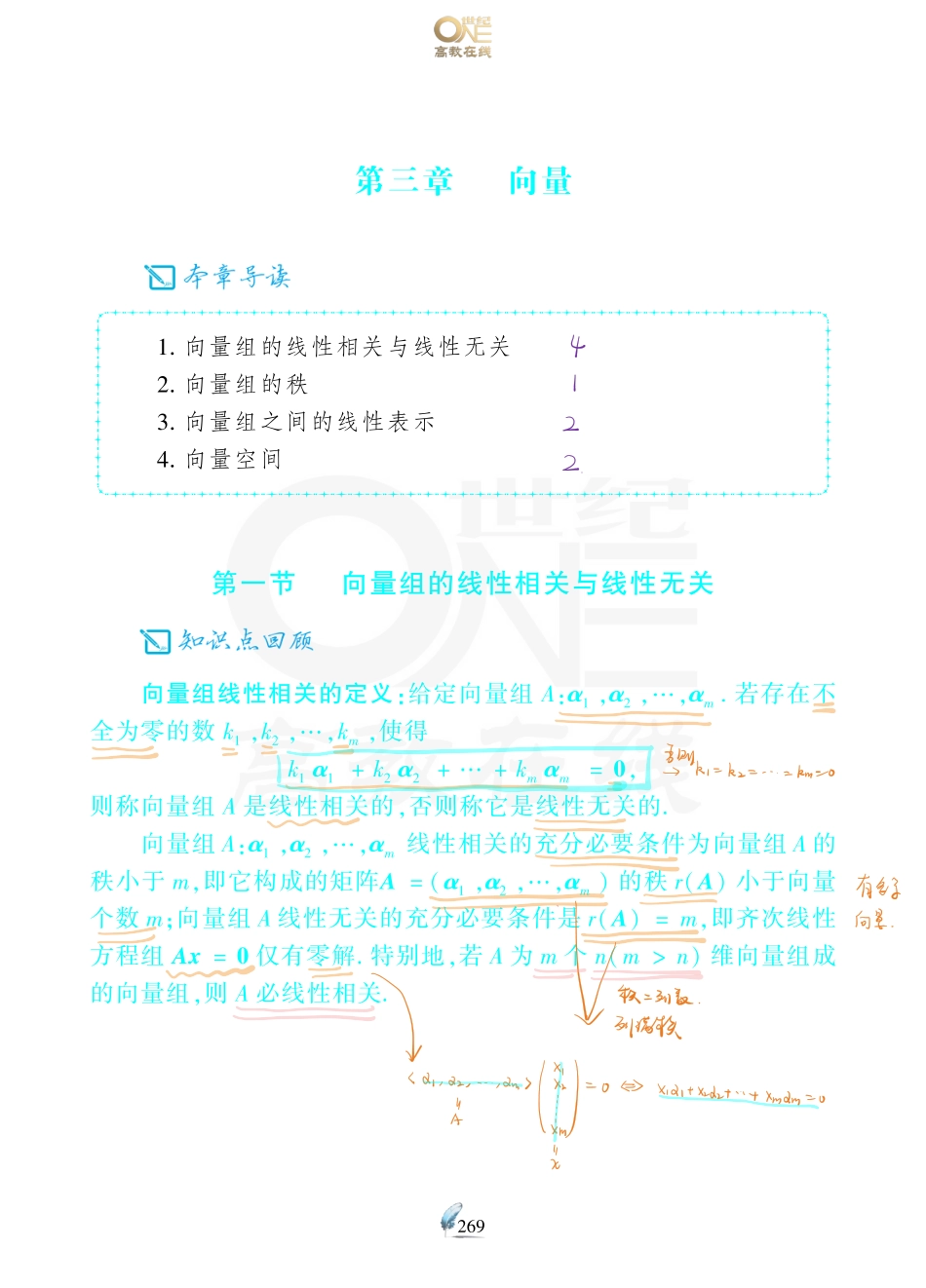
269第三章向量1.向量组的线性相关与线性无关2.向量组的秩3.向量组之间的线性表示4.向量空间第一节向量组的线性相关与线性无关向量组线性相关的定义:给定向量组A:α1,α2,…,αm.若存在不全为零的数k1,k2,…,km,使得k1α1+k2α2+…+kmαm=0,则称向量组A是线性相关的,否则称它是线性无关的.向量组A:α1,α2,…,αm线性相关的充分必要条件为向量组A的秩小于m,即它构成的矩阵A=(α1,α2,…,αm)的秩r(A)小于向量个数m;向量组A线性无关的充分必要条件是r(A)=m,即齐次线性方程组Ax=0仅有零解.特别地,若A为m个n(m>n)维向量组成的向量组,则A必线性相关.2701(1988年卷Ⅰ试题)n维向量组α1,α2,…,αs(3≤s≤n)线性无关的充分必要条件是()(A)存在一组不全为零的数k1,k2,···,ks,使k1α1+k2α2+…+ksαs≠0.(B)α1,α2,…,αs中任意两个向量都线性无关.(C)α1,α2,…,αs中存在一个向量,它不能用其余向量线性表出.(D)α1,α2,…,αs中任意一个向量都不能用其余向量线性表出.2712(1989年卷Ⅰ试题)设A是n阶矩阵,且A的行列式A=0,则A中()(A)必有一列元素全为0.(B)必有两列元素对应成比例.(C)必有一列向量是其余列向量的线性组合.(D)任一列向量是其余列向量的线性组合.2723(1994年卷Ⅰ试题)已知向量组α1,α2,α3,α4线性无关,则向量组()(A)α1+α2,α2+α3,α3+α4,α4+α1线性无关.(B)α1-α2,α2-α3,α3-α4,α4-α1线性无关.(C)α1+α2,α2+α3,α3+α4,α4-α1线性无关.(D)α1+α2,α2+α3,α3-α4,α4-α1线性无关.2734(1993年卷Ⅰ试题)设A是n×m矩阵,B是m×n矩阵,其中n<m,E是n阶单位矩阵.若AB=E,证明B的列向量组线性无关.274第二节向量组的秩1.极大线性无关组:设有向量组A,若在A中能选出α1,α2,…,αr,满足(1)向量组A0:α1,α2...