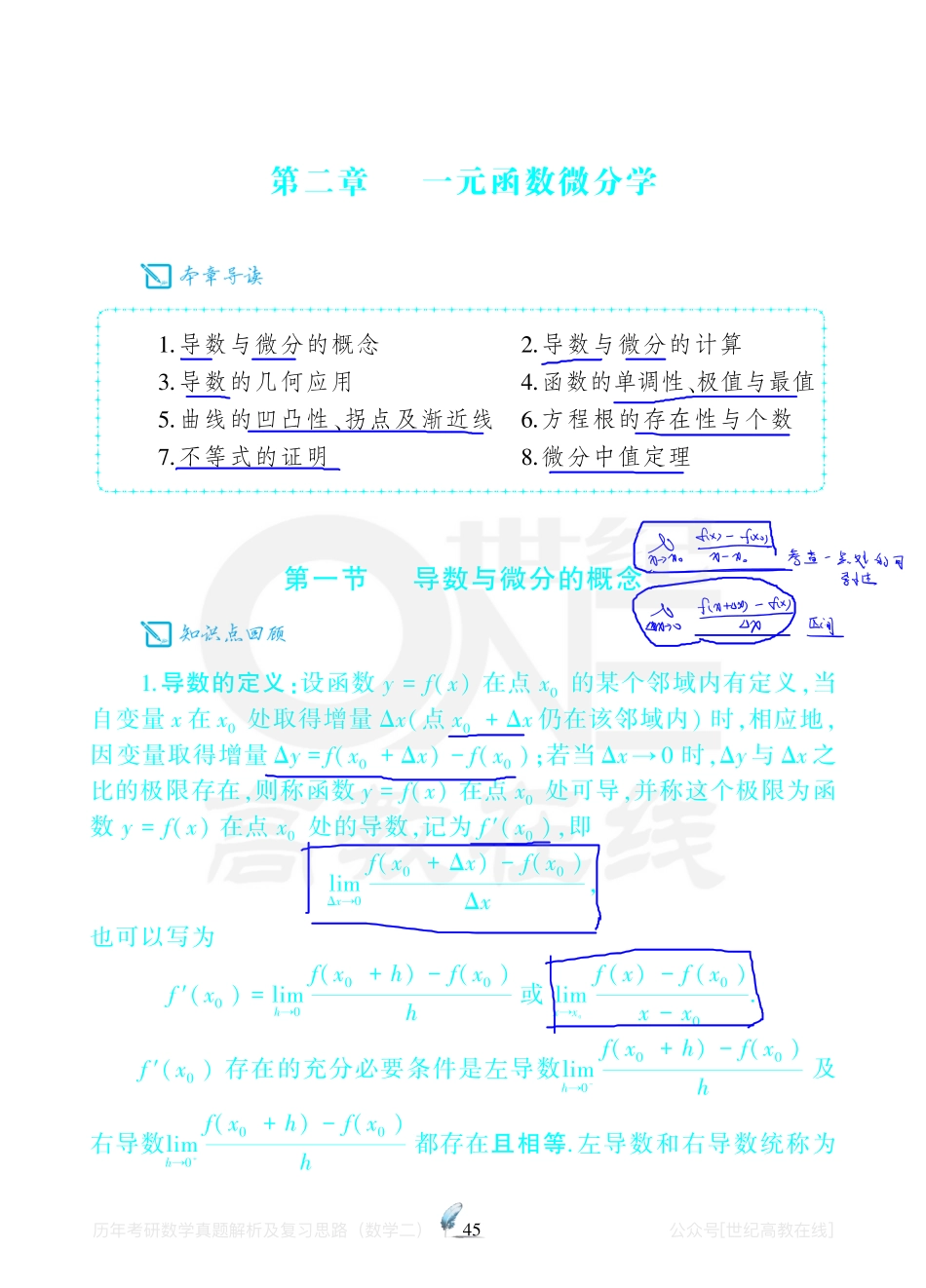
45第二章一元函数微分学������������������������������������������������������������������������������������������������������1.导数与微分的概念2.导数与微分的计算3.导数的几何应用4.函数的单调性、极值与最值5.曲线的凹凸性、拐点及渐近线6.方程根的存在性与个数7.不等式的证明8.微分中值定理第一节导数与微分的概念1.导数的定义:设函数y=f(x)在点x0的某个邻域内有定义,当自变量x在x0处取得增量Δx(点x0+Δx仍在该邻域内)时,相应地,因变量取得增量Δy=f(x0+Δx)-f(x0);若当Δx→0时,Δy与Δx之比的极限存在,则称函数y=f(x)在点x0处可导,并称这个极限为函数y=f(x)在点x0处的导数,记为f′(x0),即limΔx→0f(x0+Δx)-f(x0)Δx,也可以写为f′(x0)=limh→0f(x0+h)-f(x0)h或limx→x0f(x)-f(x0)x-x0.f′(x0)存在的充分必要条件是左导数limh→0-f(x0+h)-f(x0)h及右导数limh→0+f(x0+h)-f(x0)h都存在且相等.左导数和右导数统称为历年考研数学真题解析及复习思路(数学⼆)公众号[世纪⾼教在线]46单侧导数.2.一元函数可微的定义:设函数y=f(x)在某区间内有定义,x0及x0+Δx都在该区间内,若函数的增量Δy=f(x0+Δx)-f(x0)可表示为Δy=AΔx+o(Δx),其中A是不依赖于Δx的常数,则称函数y=f(x)在点x0是可微的,而AΔx叫做函数y=f(x)在点x0相应于自变量增量Δx的微分,记作dy,即dy=AΔx.实际上,dy=f′(x)Δx.对一元函数来说,可导即可微.历年考研数学真题解析及复习思路(数学⼆)公众号[世纪⾼教在线]47��������������������������������������题型Ⅰ:导数与微分的定义�������������������������������������������1(1987年试题)设f(x)在x=a处可导,则limx→0f(a+x)-f(a-x)x等于()(A)f′(a).(B)2f′(a).(C)0.(D)f′(2a).2(1988年试题)若函数y=f(x),有f′(x0...