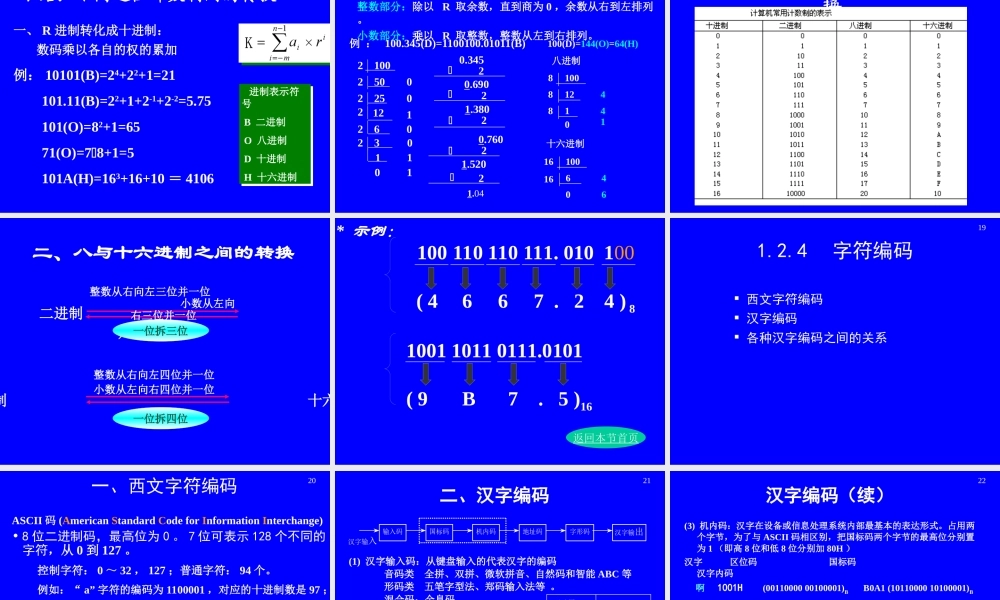
1十进制RR=10,可使用0,1,2,3,4,5,6,7,8,9二进制RR=2,可使用0,1八进制RR=8,可使用0,1,2,3,4,5,6,7十六进制RR=16,可使用0,……,9,A,B,C,D,E,F“逢RR进一一,借一一当RR”1.2.2计数制的基本概念基数:R位权:基数的若干次幂,一个数可按权展开成为多项式。(234.13)10=2×102+3×101+4×100+1×10-1+3×10-21.2.3计算机中的常用计数制及转换1、二进制(信息的存储、处理、传送)2、十六进制(书写方便)3、八进制(书写方便)4、进制间的转换1、二进制二进制数:逢2进一,基数为2,权为2的若干次幂。两个数字符号:0,1不论指令还是数据,若想存入计算机中,都必须采用二进制编码形式,在二进制系统中只有两个数0和1,即便是多媒体信息(声音、图形等)也必须转换成二进制的形式,才能存入计算机,一个二进制数在计算机中是以电子器件的两个物理状态来表示。128瓦32瓦64瓦16瓦8瓦4瓦1瓦2瓦11111111110000004二进制(续)易于物理实现,使电子线路制造计算机成为可能运算规则简单(R(R+1)/2)机器可靠性高,通用性强优点:二进制(续)二进制转换为十进制(按权展开)(10010)2=1×24+0×23+0×22+1×21+0×20=(18)10十进制转换为二进制(除2取余法)1.将十进制数除以2,得到一个商数和一个余数;2.再将商数除以2,又得到一个商数和一个余数;3.继续这个过程,直到商数等于零为止。每次得到的余数(必定是0或1)就是对应二进制数的各位数字。注意:第一次得到的余数为二进制数的最低位,最后一次得到的余数为二进制数的最高位。6例:(75)10?2结果为:10010117523712181209241220210201二进制(举例)2、十六进制十六进制数:逢16进一,基数为16,权为16的若干次幂。16个数字符号:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F一.十六进制转换为十进制(按权展开)(1CB)16=1×162+12×161+11×160=(459)10(FF)16=15×161+15×160=(255)10十六进制(续)二.十进制转换为十六进制除16取余法:1.将十进制数除以16,得到一个商数和一个余数;2.再将商数除以16,又得到一个商数和一个余数;3.继续这个过程,直到商数等于零为止。每次得到的余数(必定是0~9或A~F之一)就是对应十六进制数的各位数字。但必须注意:第一次得到的余数为十六进制数的最低位,最后一次得到的余数为十六进制数的最高位。十六进制(举例)十六进制(举例)3、八进制八进制数:逢8进一,基数为8,权为8的若干次幂。8个数字符号:0,1,2,3,4,5,6,7一.八...