数字信号处理_5 .pptVIP免费

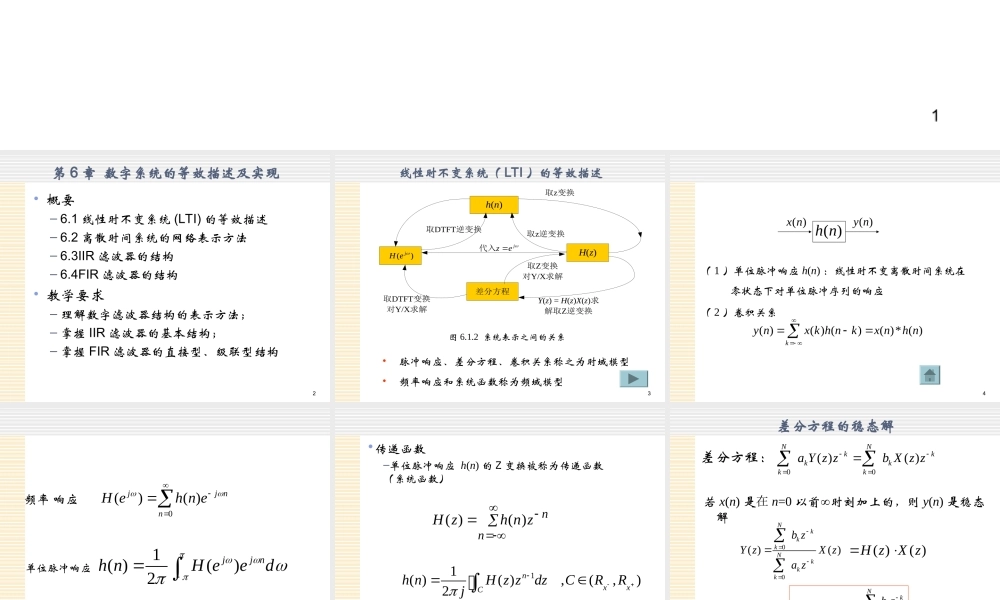
1第6章数字系统的等效描述及实现2第6章数字系统的等效描述及实现•概要–6.1线性时不变系统(LTI)的等效描述–6.2离散时间系统的网络表示方法–6.3IIR滤波器的结构–6.4FIR滤波器的结构•教学要求–理解数字滤波器结构的表示方法；–掌握IIR滤波器的基本结构；–掌握FIR滤波器的直接型、级联型结构3h(n)差分方程H(z)()jHe取z变换取z逆变换取DTFT逆变换jze代入取DTFT变换对Y/X求解取Z变换对Y/X求解Y(z)=H(z)X(z)求解取Z逆变换图6.1.2系统表示之间的关系•脉冲响应、差分方程、卷积关系称之为时域模型•频率响应和系统函数称为频域模型线性时不变系统（LTI）的等效描述4()hn()xn()yn（1）单位脉冲响应h(n)：线性时不变离散时间系统在零状态下对单位脉冲序列的响应（2）卷积关系()()()()*()kynxkhnkxnhn5频率响应0()()jjnnHehne1()()2jjnhnHeed单位脉冲响应6•传递函数–单位脉冲响应h(n)的Z变换被称为传递函数（系统函数）nnznhzH)()(11()(),(,)2nxxChnHzzdzCRRj7差分方程的稳态解若x(n)是在n=0以前时刻加上的，则y(n)是稳态解00()()NkkkNkkkbzYzXzaz()()HzXz00()()()NkkkNkkkbzYzHzXzaz00()()NNkkkkkkaYzzbXzz差分方程：8LTI系统分类01()()()1MrrrNkkkbzYzHzXzaz（1）FIR系统：ak=0,k=1,2,…,N,b0=11()1MrrrHzbz1()()()Mrrynxnbxnr单位脉冲响应有限长：h(0)=b0，h(1)=b1，…，h(M)=bM，对于n>M,h(n)=0，（2）IIR系统：ak(k=1,2,…,N)不全为零，即输入端包含输出端的反馈，此时，h(n)为无限长，故该系统称为IIR系统LTI系统：96.1.2.离散系统的零极点分析01()()()1MrrrNkkkbzYzHzXzaz11()()()MrrNkkzzHzgzp对分子、分母做因式分解g：系统的增益因子pk：系统的极点zr：系统的零点101.用系统函数的极点分布分析系统的因果性和稳定性a.因果系统：当n<0时，h(n)=0即H(z)收敛域一定包含∞点，即∞不是极点b.稳定系统：()nhn即H(z)收敛域包含单位圆c.因果且稳定系统H(z)极点集中在单位圆的内部,即H(z)收敛域r<|z|≤∞，0