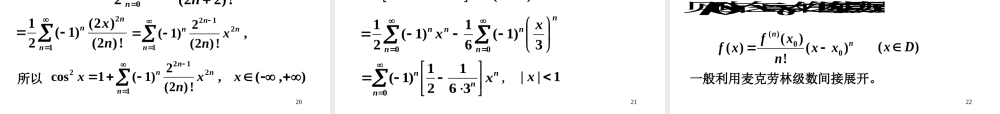第五节 函数的幂级数展开式√.pptVIP免费

1第五节函数的幂级数展开式nnnxaxf0)(求幂级数,在其收敛域内以f(x)为和函数—函数的幂级数展开。问题:2.如果能展开,是什么?na3.展开式是否唯一?1.f(x)在什么条件下才能展开成幂级数?nnnxxaxf)()(00或麦克劳林展开式泰勒展开式2函数)(xf能展开成幂级数00nnnaxx的必要条件是)(xf在点0xx处有任意阶导数，且系数定理00(),afx,01(),1!fxa02(),2!fxa()0(),!nnfxan证设函数)(xf能展开成幂级数00nnnaxx，于是存在0r,使得2010200()nnnfxaxaaxxaxx0||xxr当时3这表明)(xf是幂级数00-xnnnax在00(,)xrxr内的和函数，在上式中令0xx，即得在00()fxa.利用幂级数的和函数在其收敛区间内可任意阶求导的性质，又可得出)(xf在),(rr内有任意阶导数，101()nnnfxnaxx0(||)xxr2010200()nnnfxaxaaxxaxx01()1!fxa01()1!fxa42010200()nnnfxaxaaxxaxx202()(1)nnnfxnnaxx0(||)xxr02()2!fxa02()2!fxa303()(1)(2)nnnfxnnnaxx0(||)xxr03()3!fxa03()3!fxa52010200()nnnfxaxaaxxaxx归纳可得，()0()!kkfxak)2,1,0(k即得00(),afx,01(),1!fxa02(),2!fxa()0(),!nnfxan6泰勒中值定理0()(,)1fxxabn如果在含的区间内有直到阶的(1)10()1!nnfxxn0x其中为介于与x之间的某个数。x(,)ab连续导数，则200000(x)(x)()()(x)xx1!2!nffRxfxfxx()00(x)x!nnfxn7证明10K(x)nxx200000(x)(x)()()(x)xx1!2!nffRxfxfxx()00(x)x!nnfxn设x是某个固定的数。0()0001k000K(x)=(x)1()x!xknknxxffxxxxkx8证明10K(x)nxx以下证明200000(x)(x)()()(x)xx1!2!nffRxfxfxx()00(x)x!nnfxn设x是某个固定的数。(1)10()K(x)1!nnfxxn做辅助函数()1000k0(x)g()()xK(x)!knknftftttxk9()1000k0(x)g()()xK(x)!knknftftttxk则()0000...