第五节 函数的极值与最值(1).pptVIP免费

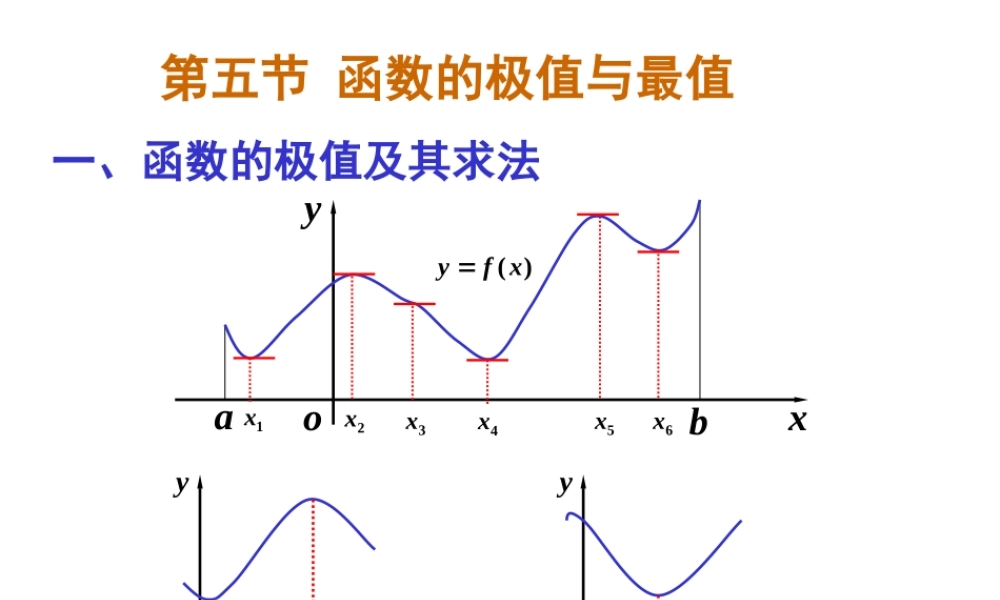
1oxyab)(xfy1x2x3x4x5x6xoxyoxy0x0x一、函数的极值及其求法第五节函数的极值与最值2设函数)(xf在0x的某个邻域),(0xU有定义,且当),(0xUx时,恒有)()(0xfxf,则称)(0xf为)(xf的一个极大值；如果当),(0xUx时,恒有)()(0xfxf,则称)(0xf为)(xf的一个极小值.定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.注：极值是局部性的概念,极大值不一定比极小值大.oxy0xoxy0x3定理1(极值的必要条件)由费马引理可知，设)(xf在点0x可导，所以对可导函数来讲,极值点必为驻点。但反之不然，驻点不一定是极值点.如3xy的驻点为0x,但它不是极值点.xyO3xy且0x是)(xf的极值点，则必有0)(0xf。4如||xy在0x处不可导,但却是极小值点.此外,不可导点也可能是极值点,xyO||xy函数的不可导点也不一定是极值点，xyO3xy如3xy在0x处不可导,却不是极值点.5这就是说,极值点要么是驻点,要么是不可导点,两者必居其一.我们把驻点和孤立的不可导点统称为极值可疑点.下面给出两个充分条件,用来判别这些极值可疑点是否为极值点.6定理2(极值的第一充分条件)xyoxyo0x0x设函数)(xf在0x处连续,在0x的某去心邻域),(0xU内可导.(1)若),(00xxx时,0)(xf,),(00xxx时,0)(xf,则0x为极大值点；(2)若),(00xxx时,0)(xf,),(00xxx时,0)(xf,则0x为极小值点；(3)如果在上述两个区间内)(xf同号,则0x不是极值点.xyoxyo0x0x一阶导数变号法7定理3(极值的第二充分判别法)设函数)(xf在它的驻点0x处二阶可导,则(1)如果0)(0xf,则0x为极小值点；(2)如果0)(0xf,则0x为极大值点；(3)如果0)(0xf,则无法判断.称为“二阶导数非零法”(1)记忆:几何直观；(3)当0)(0xf时,失效,如:43,xx在0x处.xyo0xxyo0x说明：(2)此法只适用于驻点,不能用于判断不可导点；8例1解法一.593)(23的极值求函数xxxxf963)(2xxxf，令0)(xf.3,121xx得驻点列表讨论x)1,(),3()3,1(13)(xf)(xf00极大值极小值)3(f极小值.22)1(f极大值,10,)3)(1(3xx9例1解法二.593)(23的极值求函数xxxxf963)(2xxxf，令0)(xf.3,121xx得驻点,)3)(1(3xx,66)(xxf)1(f,012；是极大值故10)1(f)3(f,012.22)3(是极小值故f10例2解.)2(1)(32的极值求出函数xxf)2()2(32)(31...