第七节 二重积分√×.pptVIP免费

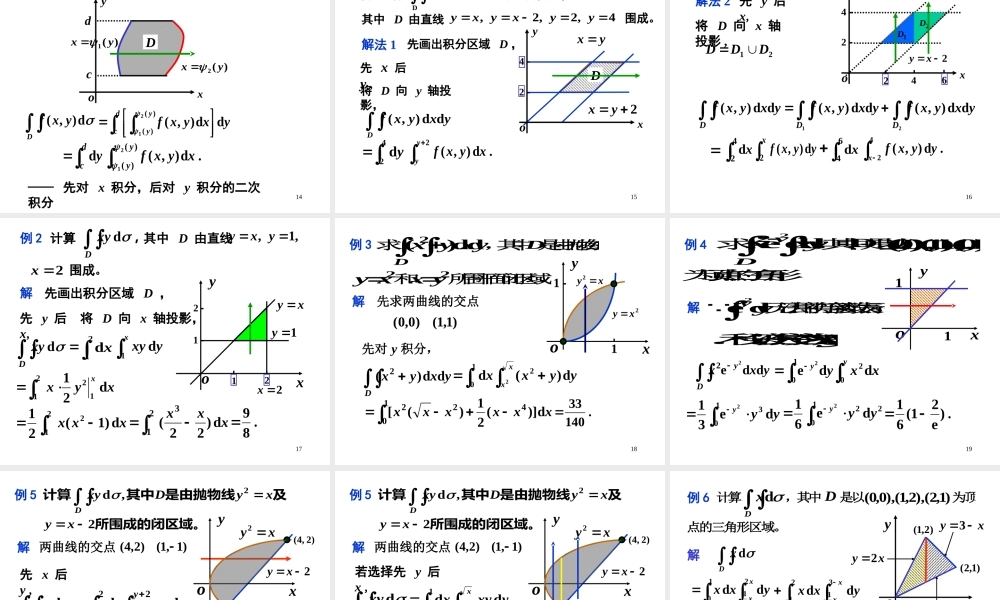
1特点：平顶.曲顶柱体体积=？特点：曲顶.),(yxfzD1、曲顶柱体的体积一、二重积分的概念柱体体积=底面积╳高第七节二重积分2播放播放求曲顶柱体的体积采用“分割、求和、取极限”的方法，如下动画演示．3步骤如下：用若干个小平顶柱体体积之和近似表示曲顶柱体的体积，xzyoD),(yxfzi),(ii先分割曲顶柱体的底，并取典型小区域，.),(lim10iiniifV曲顶柱体的体积分割取近似，iiniifV),(1极限求和42、二重积分的定义设二元函数),(yxfz是有界闭区域D上的有界函数,若将D任意分割成n个小闭区域n,,,21,并用同样的记号记它们的面积,任取iii),(,作和存在,则称函数),(yxf在D上可积,该极限称为),(yxf在D上的二重积分,记作niiiif1),(,记}{max1的直径ini,若极限niiiif10),(lim.d),(Dyxf5积分区积分区域域积分积分和和被积函被积函数数积分变积分变量量被积表达被积表达式式面积元面积元素素iiniiDfyxf),(limd),(10即6在直角坐标系下用平行于坐标轴的直线网来划分区域D，DDyxyxfyxfdd),(d),(yxddd故二重积分可写为xyoDD则面积元素为当),(yxf在闭区域上连续或分片连续时，定义中和式的极限必存在，即二重积分必存在.73、二重积分的性质下面假定f(x,y),g(x,y)在闭区域D上连续,A为D的面积.性质2线性性质DDDyxgyxfyxgyxfd),(d),(d)],(),([DDyxfkyxkfd),(d),((k为常数).若在D上1),(yxf,则由定义可知,ADd1，这里A为D的面积.性质18若0),(yxf,Dyx),(,则d|),(||d),(|DDyxfyxf性质4.0d),(Dyxf设21DDD,且21,DD无公共内点，则有性质3区域可加性.d),(d),(d),(21DDDyxfyxfyxf若),(),(yxgyxf,Dyx),(,则DDyxgyxfd),(d),(推论1推论29设),(yxf在有界闭区域D上的最大值为M,最小值为m,D的面积为A,则性质5估值性质MAyxfmADd),(证,),(Myxfmdd),(dDDDMyxfmMAyxfmADd),(所以于是10若),(yxf在D上连续,则存在一点D),(,满足:性质6(二重积分的中值定理)AfyxfD),(d),(证由性质5知,.d),(MAyxfmAD由于0A,得，MyxfAmDd),(1由闭区域上连续函数的介值定理,存在一点D),(,使，),(d),(1fyxfAD即得证...