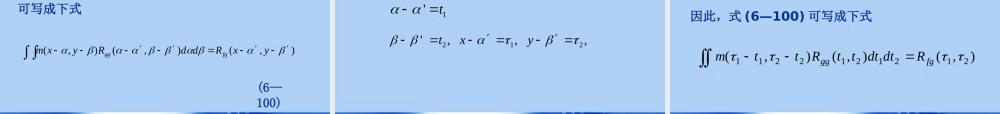第6章 图像复原（第2讲）.pptVIP免费

数字图像处理学第6章图像复原((第二讲第二讲))6.3.1最小二乘方滤波的原理6.3.2用于图像复原的几种最小二乘方滤波器设原始图像、相应的退化图像和噪声分别为f(x,y)，g(x,y)和n(x,y)。显然，它们有如下之关系式成立:gxyhxyfddnxy(,)(,)(,)(,)(6—87)式中f(x,y)，g(x,y)和n(x,y)分别为随机像场。式中噪声随机像场是不能精确知道的，但假定它的统计特性是已知的。因此，在给定了时，仍然不能精确地求解。在此，只能找出的一个估计值，使得均方误差式最小，gxy(,)fxy(,)fxy(,)(,)fxyeEfxyfxy22[(,)(,)](6—88)其中就叫给定时的最小二乘方估计。(,)fxygxy(,)fxy(,)为了便于数学处理，假定是灰度级的线性函数，那么(,)fxygxy(,)(,)(,,,)(,)fxymxygdd(6—89)这里是在计算处的时给予退化图像在点的灰度级的权重。如果随机像场是均匀的，则加权函数只与有关，所以mxy(,,,)(,)xy(,)fxy(,)(,)xy(,)(,)(,)fxymxygdd(6—90)将式(6—90)代入式(6—88)，则:22),(),(),(ddgyxmyxfEe(6—91)显然，需要寻求使最小的点扩散函数。e2mxy(,)可以证明，对于xy平面上所有的位置向量(x,y)和都满足下式),(βα0)(),(),(),(βαgβdαdβαgβyαxmyxfE(6—92)的函数将使式(6—91)最小。设是一个满足式(6—92)的函数。任选一个其他函数，其均方误差由下式表示mxy(,)),(yxm22),(),(),(βdαdβαgβyαxmyxfEe(6—93)现在可证明时，使),(),(yxmyxm22),(),(),(βdαdβαgβyαxmyxfEe最小。222(,)(,)(,)(,)(,)(,)(,)(,)(,)eEfxymxygddEfxymxygddmxymxygdd(6—94)将式(6—93)改写于下22(,)(,)(,)+E(,)(,)(,)2(,)(,)(,)[(,)(,)](,)EfxymxygddmxymxygddEfxymxygddmxymxygdd(6—94)由式(6—94)可见，第一项就是，第二项总是大于零的项，所以，可写作e2(6—95)}),(),(),([),(),(),({222ddgyxmyxmddgyxmyxfEee...