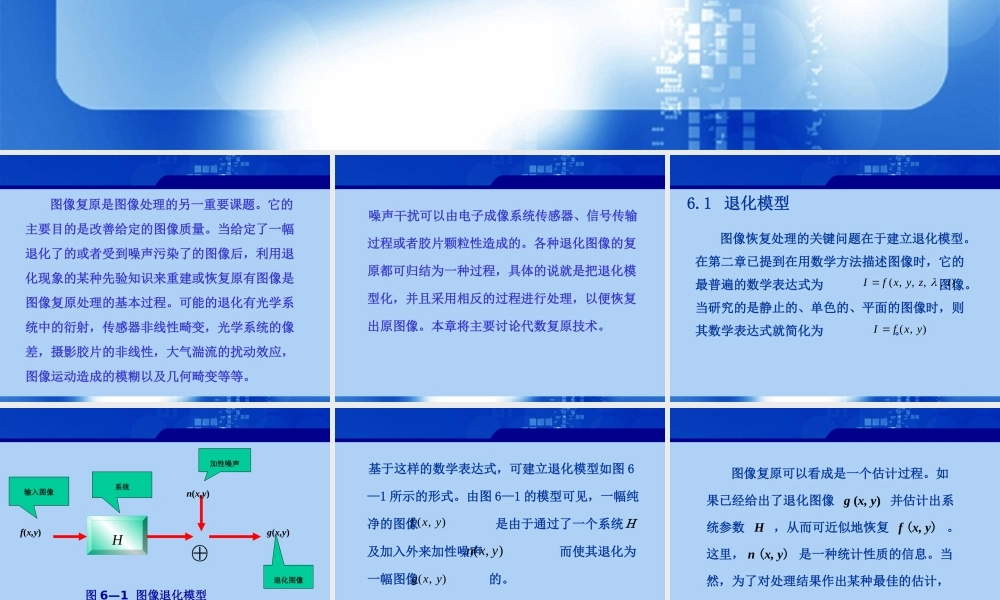
数字图像处理学第6章图像复原((第一讲第一讲))图像复原是图像处理的另一重要课题。它的主要目的是改善给定的图像质量。当给定了一幅退化了的或者受到噪声污染了的图像后,利用退化现象的某种先验知识来重建或恢复原有图像是图像复原处理的基本过程。可能的退化有光学系统中的衍射,传感器非线性畸变,光学系统的像差,摄影胶片的非线性,大气湍流的扰动效应,图像运动造成的模糊以及几何畸变等等。噪声干扰可以由电子成像系统传感器、信号传输过程或者胶片颗粒性造成的。各种退化图像的复原都可归结为一种过程,具体的说就是把退化模型化,并且采用相反的过程进行处理,以便恢复出原图像。本章将主要讨论代数复原技术。6.1退化模型图像恢复处理的关键问题在于建立退化模型。在第二章已提到在用数学方法描述图像时,它的最普遍的数学表达式为图像。当研究的是静止的、单色的、平面的图像时,则其数学表达式就简化为。Ifxyzt(,,,,)Ifxy(,)H⊕f(x,y)g(x,y)n(x,y)图6—1图像退化模型输入图像系统加性噪声退化图像基于这样的数学表达式,可建立退化模型如图6—1所示的形式。由图6—1的模型可见,一幅纯净的图像是由于通过了一个系统H及加入外来加性噪声而使其退化为一幅图像的。fxy(,)),(yxngxy(,)图像复原可以看成是一个估计过程。如果已经给出了退化图像g(x,y)并估计出系统参数H,从而可近似地恢复f(x,y)。这里,n(x,y)是一种统计性质的信息。当然,为了对处理结果作出某种最佳的估计,一般应首先明确一个质量标准。6.1.1系统的基本定义6.1.2连续函数退化模型6.1.3离散的退化模型H根据图像的退化模型及复原的基本过程可见,复原处理的关键在于对系统H的基本了解。就一般而言,系统是某些元件或部件以某种方式构造而成的整体。系统本身所具有的某些特性就构成了通过系统的输入信号与输出信号的某种联系。系统的分类方法很多。例如,系统可分为线性系统和非线性系统;时变系统和非时变系统;集中参数系统和分布参数系统;连续系统和离散系统等等。H⊕f(x,y)g(x,y)n(x,y)图6—1图像退化模型线性系统就是具有均匀性和相加性的系统。对于图6—1所示的系统来说,可表示成下式),(),(),(yxnyxfHyxg(6—1)),(),(yxfHyxg(6—2)如果暂不考虑加性噪声n(x,y)的影响,而令时,则n(x,y)=0如果输入信号为,,对应的输出信号为,,通过系统后有下式成立fxy1(,)fxy2(,)gxy1(,)gxy2(,)),(),(),(),(),(),(221122112211yxgk...