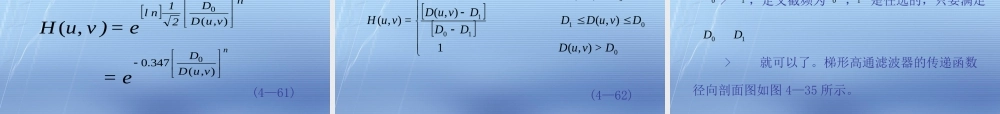第4章 图像增强(第4讲).pptVIP免费

数字图像处理学第4章图像增强(第四讲)4.3.1微分尖锐化处理4.3.2高通滤波法4.3.1微分尖锐化处理4.3.32高通滤波法因为图像中的边缘及急剧变化部分与高频分量有关，所以当利用高通滤波器衰减图像信号中的低频分量时就会相对地强调其高频分量，从而加强了图像中的边缘及急剧变化部分，达到图像尖锐化的目的。与低通滤波器相对应，常用的高通滤波器有理想高通滤波器、布特沃斯高通滤波器、指数高通滤波器和梯形高通滤波器等。这里只讨论径向对称的零相移滤波器。理想高通滤波器布特沃斯（Butterworth）高通滤波器指数高通滤波器梯形高通滤波器(4—56)理想高通滤波器一个理想的二维高通滤波器的传递函数由下式表示00),(1),(0),(DvuDDvuDvuH式中是从频度平面原点算起的截止频率(或距离)，仍然由下式决定D0),(vuD2122=),D(vuvu(4—57)理想高通滤波器传递函数的剖面图如图4—32所示：图4—28理想高通滤波器传递函数径向剖面图由图可见，理想高通传递函数与理想低通正好相反。通过高通滤波正好把以为半径的圆内的频率成分衰减掉，对圆外的频率成分则无损地通过。与理想低通一样，理想高通可以用计算机模拟实现，但不可能用电子元件来实现。D0布特沃斯（Butterworth）高通滤波器截止频率为的阶布特沃斯高通滤波器的传递函数如下式表示D0nvuDDvuH20),(+11=),((4—58)式中2122=),D(vuvun布特沃斯高通滤波器传递函数的径向剖面图如图4—33所示：图4—29布特沃斯高通滤波器传递函数径向剖面图(n=1)与低通滤波器一样，定下降到其最大值的处的为截频点。一般情况下，高通滤波器的截频选择在使下降到其最大值的处，满足这一条件的传递函数可修改成下式),(vuH12),(vuDD0),(vuH12nnvuDDvuDDuH2020),(0.414+11=),(12+11=v),((4—59)指数高通滤波器截频为的指数高通滤波器的传递函数如下式表示D0nvuDD-e=)vuH),(0,((4—60)式中为截频，，参数控制着的增长率。指数高通滤波器的传递函数径向剖面图如图4—34所示。D02122=),D(vuvu),(vuHn图4—30指数高通滤波器传递函数径向剖面图由式(4—60)可知，当时，。如果仍然把截止频率定在最大值的时，则其传递函数可修改为下面的形式：0D=),(vuDevuH1=),(),(vuH12nvuDDnvuDD21nle=e=)vuH),(347.0),(00,((4—61)梯形高通滤波器梯形高通滤波器的传递函数用下式表示...