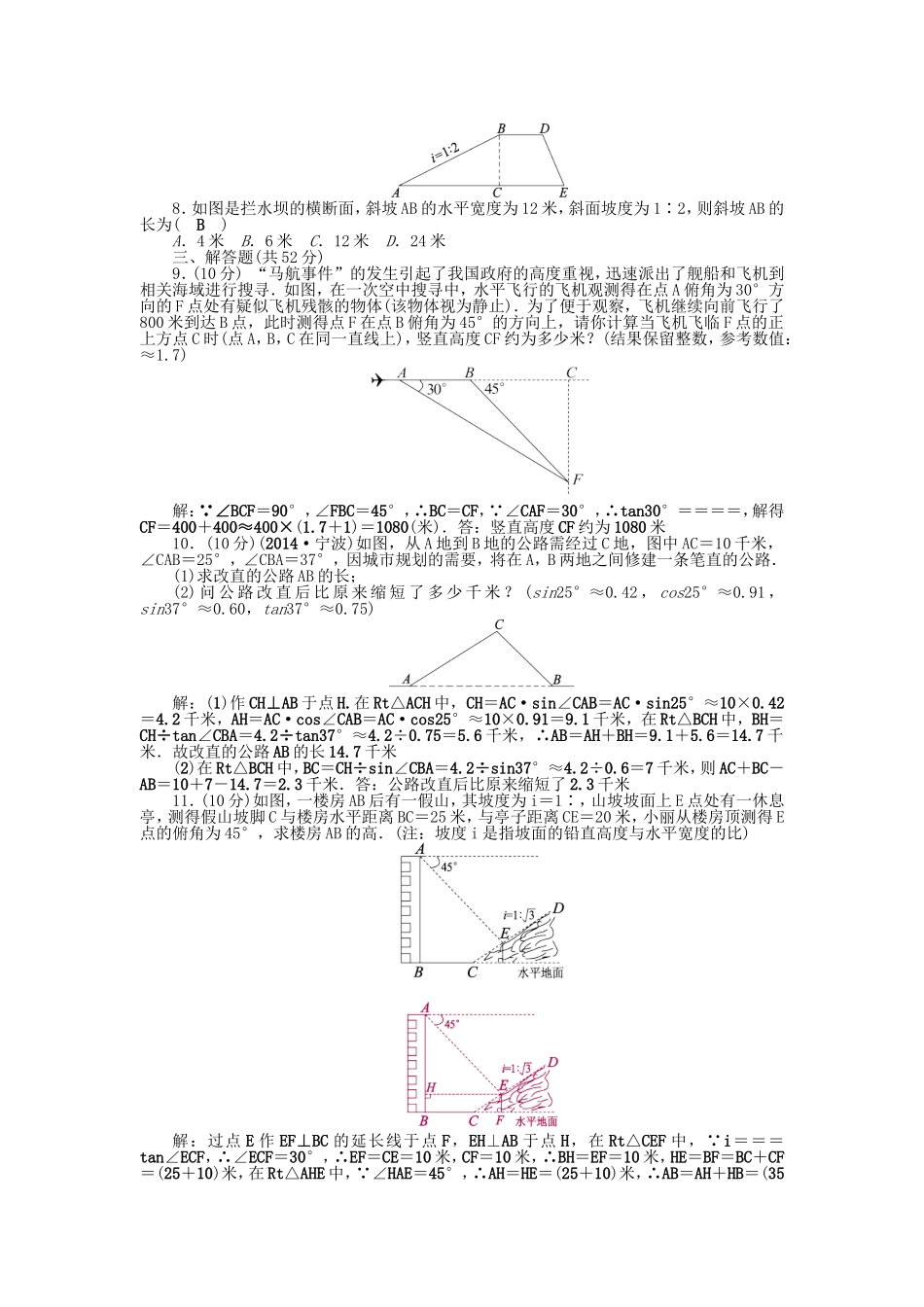
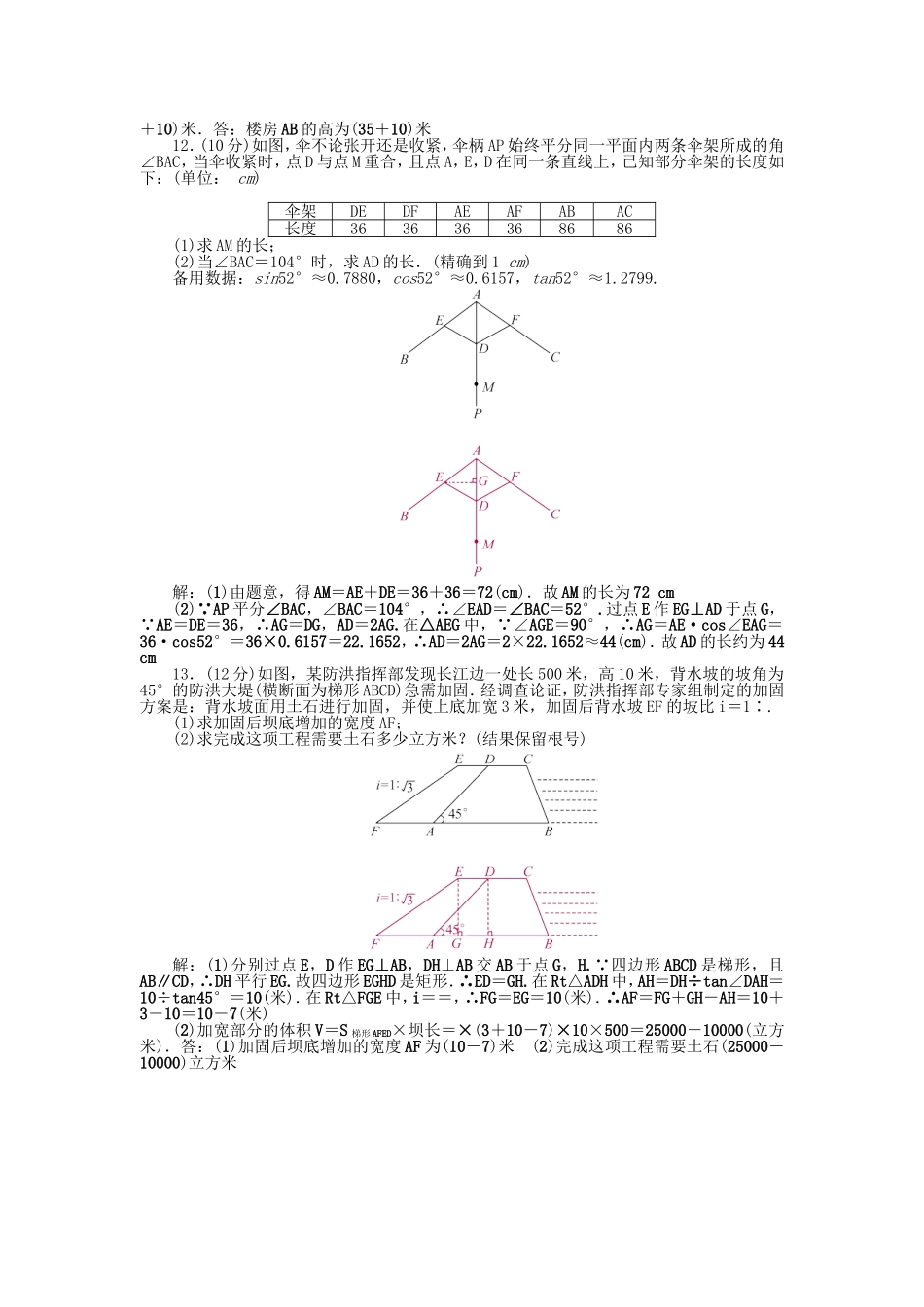
第23章解直角三角形检测题一、填空题(每小题6分,共24分)1.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是____.2.在Rt△ABC中,∠C=90°,tanA=,BC=8,则△ABC的面积为__24__.3.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为__7tanα__米.(用含α的代数式表示)4.为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(≈1.4)解析:如下图,BC=2.2×sin45°=2.2×≈1.54米,CE=5×sin45°=5×≈3.5米,BE=BC+CE≈5.04,EF=2.2÷sin45°=2.2÷≈3.14米,(56-5.04)÷3.14+1=50.96÷3.14+1≈16+1=17(个).故这个路段最多可以划出17个这样的停车位二、选择题(每小题6分,共24分)5.在Rt△ACB中,∠C=90°,AB=10,sinA=,cosA=,tanA=,则BC的长为(A)A.6B.7.5C.8D.12.56.如图,在下列网格中,小正方形的边长均为1,点A,B,O都在格点上,则∠AOB的正弦值是(D)A.B.C.D.7.在△ABC中,若|cosA-|+(1-tanB)2=0,则∠C的度数是(C)A.45°B.60°C.75°D.105°8.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1∶2,则斜坡AB的长为(B)A.4米B.6米C.12米D.24米三、解答题(共52分)9.(10分)“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为45°的方向上,请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:≈1.7)解: ∠BCF=90°,∠FBC=45°,∴BC=CF, ∠CAF=30°,∴tan30°====,解得CF=400+400≈400×(1.7+1)=1080(米).答:竖直高度CF约为1080米10.(10分)(2014·宁波)如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.(1)求改直的公路AB的长;(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)解:(1)作CH⊥AB于点H.在Rt△ACH中,CH=AC·sin∠CAB=AC·sin25°≈10×0.42=4.2千米,AH=AC·cos...