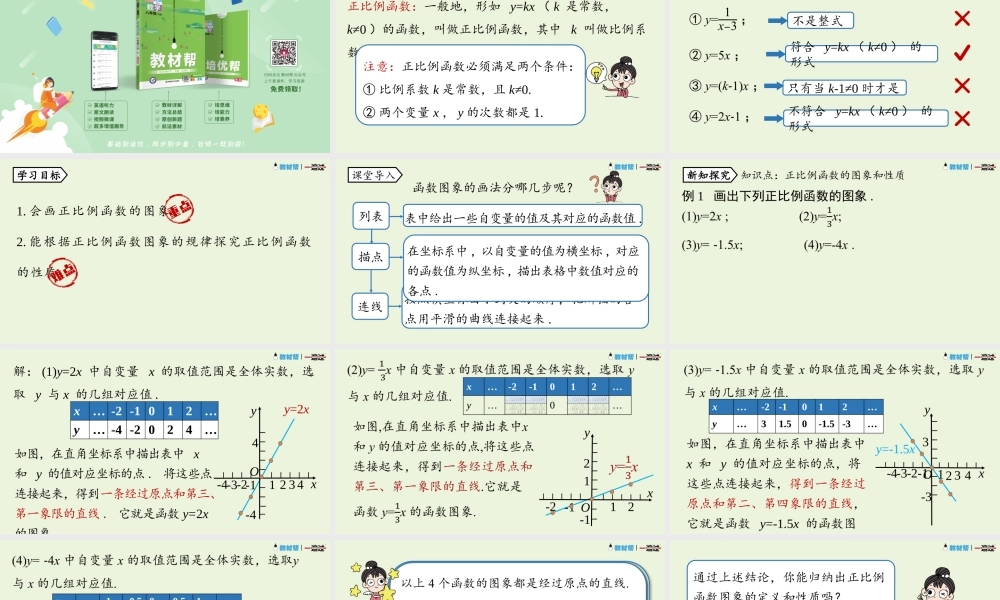
一次函数八年级下册RJ初中数学19.2.1正比例函数课时2正比例函数:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.注意:正比例函数必须满足两个条件:①比例系数k是常数,且k≠0.②两个变量x,y的次数都是1.知识回顾判断下列函数关系式是不是正比例函数.不是整式只有当k-1≠0时才是符合y=kx(k≠0)的形式不符合y=kx(k≠0)的形式1.会画正比例函数的图象.2.能根据正比例函数图象的规律探究正比例函数的性质.学习目标表中给出一些自变量的值及其对应的函数值.按照横坐标由小到大的顺序,把所描的各点用平滑的曲线连接起来.函数图象的画法分哪几步呢?课堂导入描点列表连线在坐标系中,以自变量的值为横坐标,对应的函数值为纵坐标,描出表格中数值对应的各点.例1画出下列正比例函数的图象.知识点:正比例函数的图象和性质新知探究y=2x如图,在直角坐标系中描出表中x和y的值对应坐标的点.将这些点连接起来,得到一条经过原点和第三、第一象限的直线.它就是函数y=2x的图象O12344-4-3-2-1xy解:(1)y=2x中自变量x的取值范围是全体实数,选取y与x的几组对应值.x…-2-1012…y…-4-2024…-4x…-2-1012…y…0…O1212-2-1xy-1y=-1.5xO1234-33-4-3-2-1xyx…-2-1012…y…31.50-1.5-3…如图,在直角坐标系中描出表中x和y的值对应坐标的点,将这些点连接起来,得到一条经过原点和第二、第四象限的直线,它就是函数y=-1.5x的函数图x…-1-0.500.51…y…420-2-4…y=-4xO1224-2-1xy-4-2如图,在直角坐标系中描出表中x和y的值对应坐标的点,将这些点连接起来,得到一条经过原点和第二、第四象限的直线,它就是函数y=-4x的函数图1.正比例函数的图象:一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.通过上述结论,你能归纳出正比例函数图象的定义和性质吗?2.正比例函数图象的性质当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.注意:正比例函数图象的位置和函数的增减性只与k的正负有关.思考画正比例函数的图象时,怎样画最简单?为什么?3.正比例函数图象的画法:因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图象.一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图象.A.k>0B.k<0C.k>2D.k<2DxyO跟踪训练新知探究经过第二、第四象...