《二次函数的应用（3）》教学课件.pptVIP免费

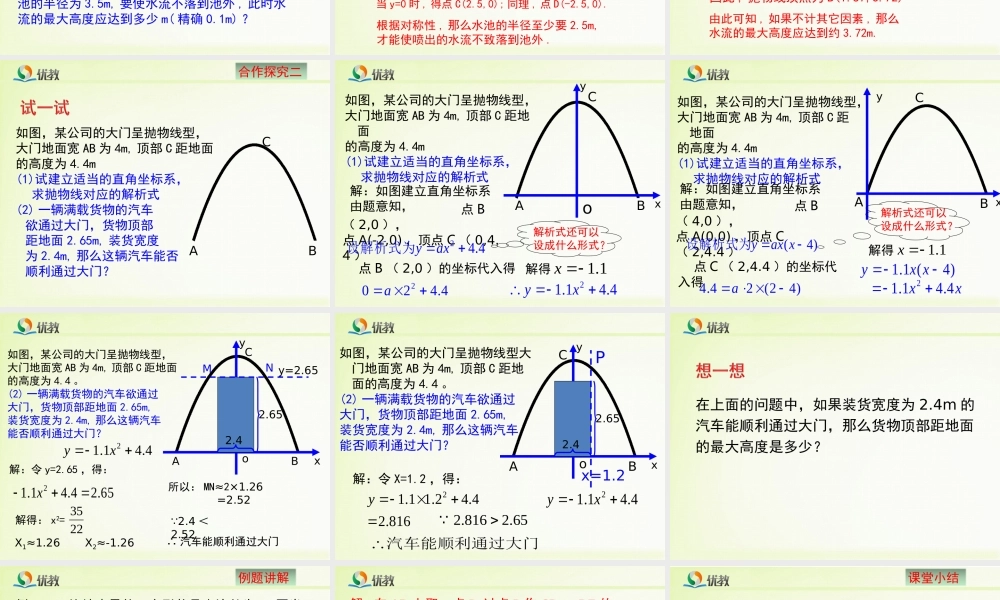
第三章二次函数6.二次函数的应用（3）Contents目录01020304课堂小结05例题讲解合作探究一旧知回顾合作探究二旧知回顾二次函数应用的思路1.理解问题;2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.运用数学知识求解;5.检验结果的合理性,给出问题的解答.合作探究一喷泉与二次函数做一做：公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到最大高度2.25m.(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外？(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确0.1m)？解:(1)如图,建立如图所示的坐标系,25.212xy当y=0时,得点C(2.5,0);同理,点D(-2.5,0).设抛物线为y=a(x-1)2+2.25,由待定系数法可求得抛物线表达式为:y=-(x-1)2+2.25.数学化xyOA●B(1,2.25)●(0,1.25)●C(2.5,0)●D(-2.5,0)根据题意得,A(0,1.25),顶点B(1,2.25).根据对称性,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.数学化xyOA●B(1.57,3.72)●(0,1.25)●C(3.5,0)●D(-3.5,0)解:(2)根据题意得,A(0,1.25),C(3.5,0).由此可知,如果不计其它因素,那么水流的最大高度应达到约3.72m.设抛物线为y=-(x-h)2+k,由待定系数法求得抛物线为:y=-(x-11/7)2+729/196.因此,抛物线顶点为B(1.57,3.72)合作探究二如图，某公司的大门呈抛物线型，大门地面宽AB为4m,顶部C距地面的高度为4.4m(1)试建立适当的直角坐标系，求抛物线对应的解析式(2)一辆满载货物的汽车欲通过大门，货物顶部距地面2.65m,装货宽度为2.4m,那么这辆汽车能否顺利通过大门？ABC如图，某公司的大门呈抛物线型，大门地面宽AB为4m,顶部C距地面的高度为4.4m(1)试建立适当的直角坐标系，求抛物线对应的解析式ABCoyx解：如图建立直角坐标系由题意知，点B（2,0），点A(-2,0)，顶点C（0,4.4）24.4yax设解析式为点B（2,0）的坐标代入得2024.4a解得1.1x21.14.4yx解析式还可以设成什么形式？yxABC如图，某公司的大门呈抛物线型，大门地面宽AB为4m,顶部C距地面的高度为4.4m(1)试建立适当的直角坐标系，求抛物线对应的解析式解：如图建立直角坐标系由题意知，点B（4,0），点A(0,0)，顶点C（2,4.4）...