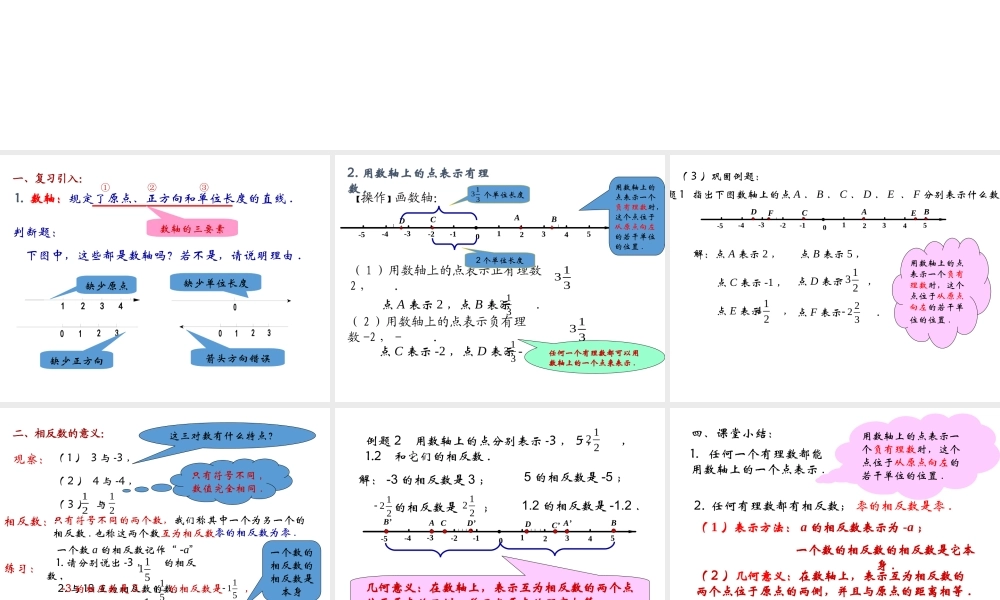
5.2数轴一、复习引入:1.数轴:规定了原点、正方向和单位长度的直线.判断题:下图中,这些都是数轴吗?若不是,请说明理由.4321032103210缺少原点箭头方向错误缺少正方向缺少单位长度数轴的三要素①②③2.用数轴上的点表示有理数.【操作】画数轴:(1)用数轴上的点表示正有理数2,.133点A表示2,点B表示.133(2)用数轴上的点表示负有理数-2,-.133点C表示-2,点D表示-.133133个单位长度2个单位长度任何一个有理数都可以用数轴上的一个点来表示.-5-4-3-2-1543210用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.ABCD(3)巩固例题:题1指出下图数轴上的点A、B、C、D、E、F分别表示什么数142点E表示,132点D表示,223点F表示.解:点A表示2,点B表示5,点C表示-1,用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.-5-4-3-2-1543210AFECBD二、相反数的意义:观察:(1)3与-3,(2)4与-4,1212(3)与.这三对数有什么特点?只有符号不同,数值完全相同.只有符号不同的两个数,我们称其中一个为另一个的相反数.也称这两个数互为相反数.相反数:练习:1.请分别说出-3,的相反数,1153.请分别说出-3,的相反数的相反数,1152.与18互为相反数的数,-3的相反数是3,的相反数是,115115与18互为相反数的数是-18,-3的相反数的相反数是3,一个数的相反数的相反数是本身零的相反数为零.一个数a的相反数记作“-a”的相反数的相反数是,115115-5-4-3-2-1543210122例题2用数轴上的点分别表示-3,5,,1.2和它们的相反数.解:-3的相反数是3;5的相反数是-5;1.2的相反数是-1.2.的相反数是;122122几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.三、课堂练习:课本P7,练习5.2ACBDA’B’C’D’四、课堂小结:1.任何一个有理数都能用数轴上的一个点表示.用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.2.任何有理数都有相反数;零的相反数是零.(2)几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.012345-1-2-3-4-5(1)表示方法:a的相反数表示为-a;一个数的相反数的相反数是它本身.补充题:1、一个数的相反数是它本身,这个数是______;2、一个数的倒数是它本身,这个数是_______;3、x-3的相反数是3,则x=________;﹡4、a是最小的自然数,b是最小的正整数,c和d互为相反数,e是3的倒数,a+b+c+d+e=___.01或-10a=0b=1c+d=0e=3134再见