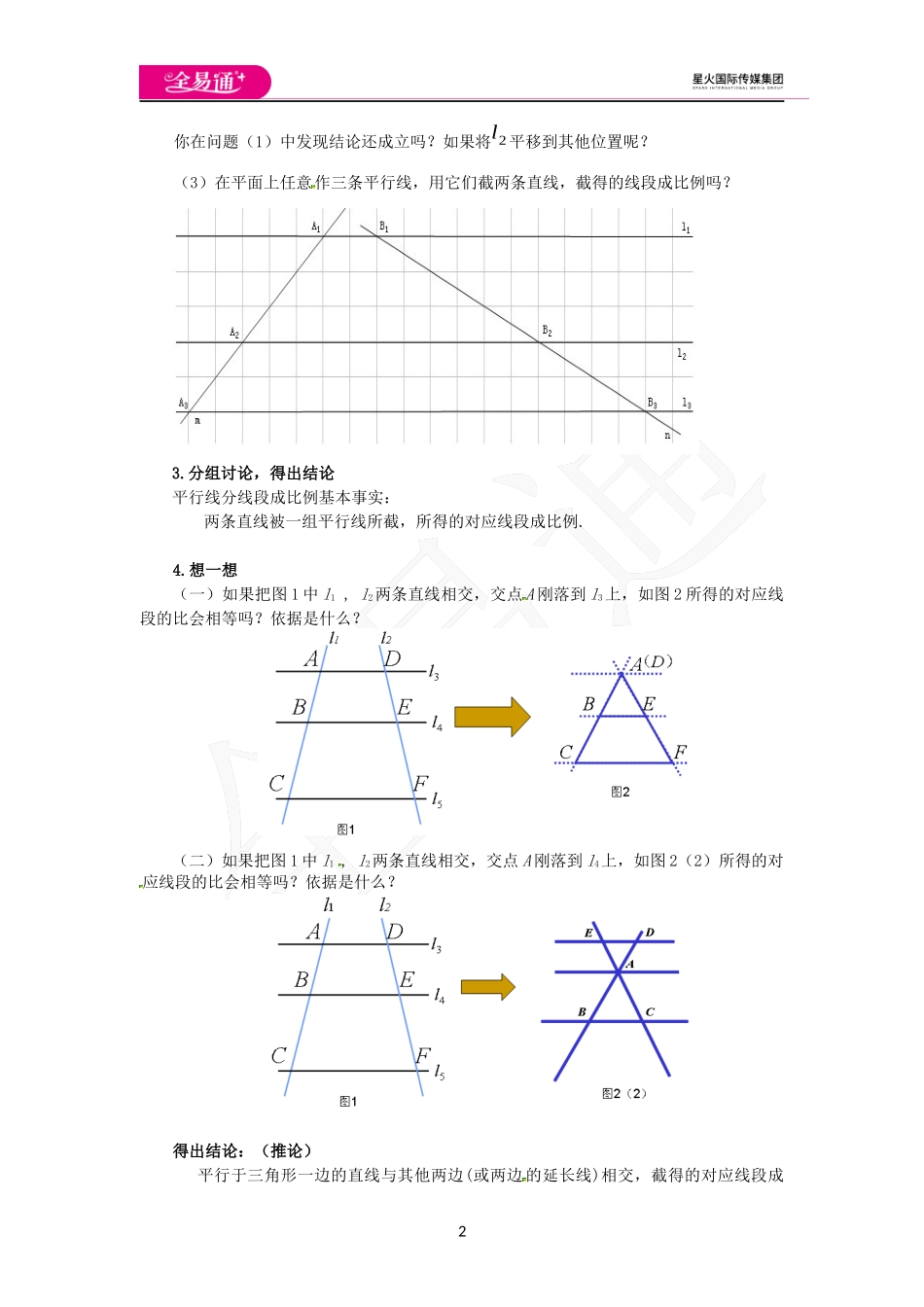
11.2怎样判定三角形相似(1)教学目标【知识与能力】1.了解平行线分线段成比例基本事实及其推论..2.会用平行线分线段成比例解决实际问题.【过程与方法】借助方格纸,通过观察、计算,由特殊到一般地逐步归纳、猜想,进而明确平行线分线段成比例的基本事实;然后把这一基本事实特殊化(应用在三角形中),得到推论,为后面证明相似三角形的判定基本事实做准备.【情感态度价值观】掌握推理证明的方法,发展演绎推理能力课前准备课件、方格纸.教学过程1.情景导入梯子是我们生活中常见的工具.如图是一个生产过程中不合格的左右不对称的梯子的简图,经测量,AB=BC=CD,AA1∥BB1∥CC1∥DD1,那么A1B1和B1C1相等吗?2.新知探究在图4-6中,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n与格点A1,A2,A3,B1,B2,B3.图4-6(1)计算的值,你有什么发现?(2)将l2向下平移到如图4-7的位置,直线m,n与l2的交点分别为A1,B22你在问题(1)中发现结论还成立吗?如果将l2平移到其他位置呢?(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?3.分组讨论,得出结论平行线分线段成比例基本事实:两条直线被一组平行线所截,所得的对应线段成比例.4.想一想(一)如果把图1中l1,l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?(二)如果把图1中l1,l2两条直线相交,交点A刚落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?得出结论:(推论)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成3比例.5.例题学习探究点一:平行线分线段成比例如图,直线l1∥l2∥l3,直线AC分别交这三条直线于点A,B,C,直线DF分别交这三条直线于点D,E,F,若AB=3,DE=,EF=4,求BC的长.解: 直线l1∥l2∥l3,且AB=3,DE=,EF=4,∴根据平行线分线段成比例可得=,即BC=·AB=×3=.方法总结:利用平行线分线段成比例求线段长的方法:先确定图中的平行线,由此联想到线段之间的比例关系,结合待求线段和已知线段写出一个含有它们的比例关系式,构造出方程,解方程求出待求线段长.如图所示,直线l1∥l2∥l3,下列比例式中成立的是()A.=B.=C.=D.=解析:由平分线分线段成比例可知=,故A选项不成立;由=可知B选项不成立;由=可知C选项不成立;D选项成立.故选D.方法总结:应用平行线分线段成比例得到的比例式中,四条线段与两条直线的交点位置无关,关键是线段的...