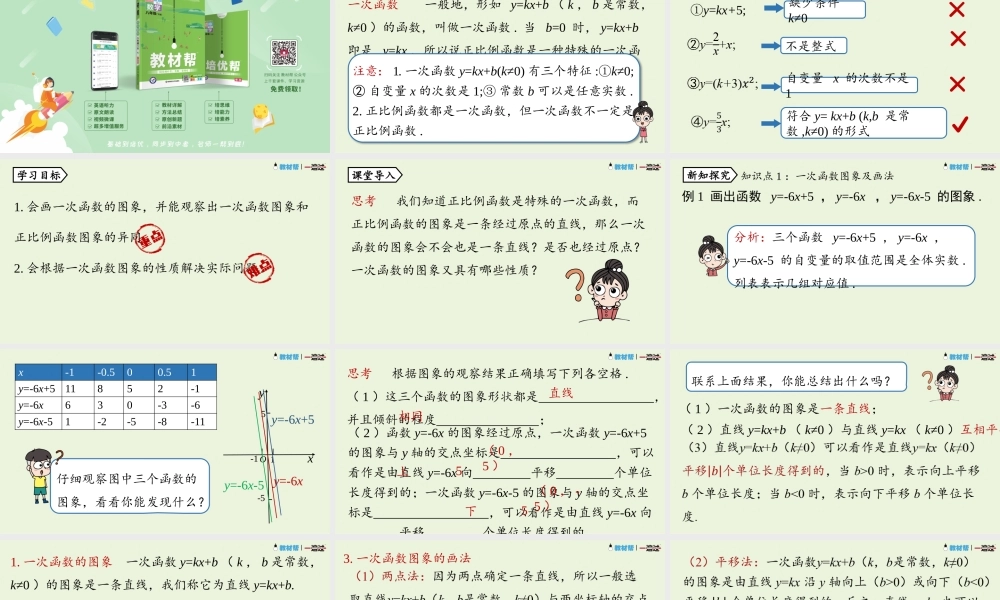
一次函数八年级下册RJ初中数学19.2.2一次函数课时2一次函数一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即是y=kx,所以说正比例函数是一种特殊的一次函数.知识回顾注意:1.一次函数y=kx+b(k≠0)有三个特征:①k≠0;②自变量x的次数是1;③常数b可以是任意实数.2.正比例函数都是一次函数,但一次函数不一定是正比例函数.判断下列函数关系式是不是一次函数.①y=kx+5;不是整式缺少条件k≠0自变量x的次数不是1符合y=kx+b(k,b是常数,k≠0)的形式1.会画一次函数的图象,并能观察出一次函数图象和正比例函数图象的异同.2.会根据一次函数图象的性质解决实际问题.学习目标思考我们知道正比例函数是特殊的一次函数,而正比例函数的图象是一条经过原点的直线,那么一次函数的图象会不会也是一条直线?是否也经过原点?一次函数的图象又具有哪些性质?课堂导入例1画出函数y=-6x+5,y=-6x,y=-6x-5的图象.知识点1:一次函数图象及画法新知探究分析:三个函数y=-6x+5,y=-6x,y=-6x-5的自变量的取值范围是全体实数.列表表示几组对应值.yxOy=-6x+5y=-6x-5y=-6x5-51-1x-1-0.500.51y=-6x+511852-1y=-6x630-3-6y=-6x-51-2-5-8-11仔细观察图中三个函数的图象,看看你能发现什么?思考根据图象的观察结果正确填写下列各空格.(1)这三个函数的图象形状都是,并且倾斜的程度;(2)函数y=-6x的图象经过原点,一次函数y=-6x+5的图象与y轴的交点坐标是,可以看作是由直线y=-6x向平移个单位长度得到的;一次函数y=-6x-5的图象与y轴的交点坐标是,可以看作是由直线y=-6x向平移个单位长度得到的直线相同(0,5)上5(0,-5)下5(2)直线y=kx+b(k≠0)与直线y=kx(k≠0)互相平行(1)一次函数的图象是一条直线;联系上面结果,你能总结出什么吗?1.一次函数的图象一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线,我们称它为直线y=kx+b.xyOy=kx+b(0,b)3.一次函数图象的画法xyOy=kx分析:由于一次函数的图象是直线,因此只要确定两个点就能画出它们.例2画出函数y=2x-1与y=-0.5x+1的图象.过点(0,-1)与点(1,1)画出直线y=2x-1;过点(0,1)与点(1,0.5)画出直线y=-0.5x+1.y=2x-1y=-0.5x+1x01y=2x-1-11y=-0.5x+110.5解:列表表示当x=0,x=1时两个函数的对应值.探究画出函数y=x+2和y=-x+2的图象.由它们联想:一次函数解析式y=kx+b(k,b是常数,k≠0)中,k的正负对函数图象有什么影响?y=x+2与坐标轴的交点坐标分别为(0,2)和(-2,0);y=-x...