22.1 第3课时比例的性质和黄金分割.pptxVIP免费

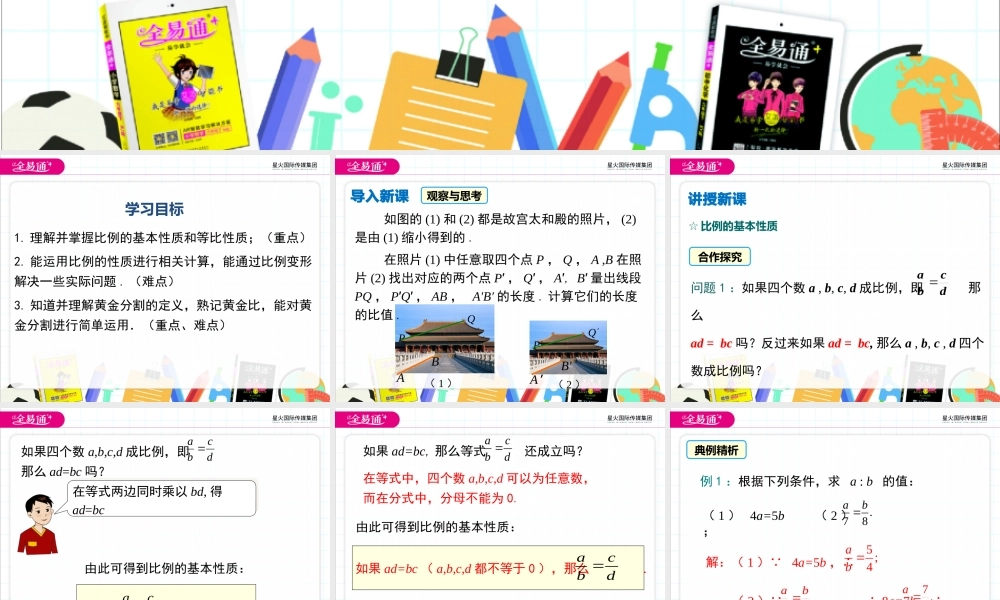
第22章相似形22.1比例线段第3课时比例的性质与黄金分割1.理解并掌握比例的基本性质和等比性质；（重点）2.能运用比例的性质进行相关计算，能通过比例变形解决一些实际问题.（难点）3.知道并理解黄金分割的定义，熟记黄金比，能对黄金分割进行简单运用．（重点、难点）学习目标导入新课观察与思考如图的(1)和(2)都是故宫太和殿的照片，(2)是由(1)缩小得到的.（1）（2）PQP′Q′在照片(1)中任意取四个点P，Q，A,B在照片(2)找出对应的两个点P′，Q′，A′,B′量出线段PQ，P′Q′，AB，A′B′的长度.计算它们的长度的比值.AA'B'B讲授新课☆比例的基本性质合作探究问题1：如果四个数a,b,c,d成比例，即那么ad=bc吗？反过来如果ad=bc,那么a,b,c,d四个数成比例吗？dcba如果四个数a,b,c,d成比例，即那么ad=bc吗？dcba在等式两边同时乘以bd,得ad=bc在等式两边同时乘以bd,得ad=bc由此可得到比例的基本性质：如果，那么ad=bc.dcba由此可得到比例的基本性质：如果ad=bc（a,b,c,d都不等于0），那么.dcba如果ad=bc,那么等式还成立吗？acbd在等式中，四个数a,b,c,d可以为任意数，而在分式中，分母不能为0.典例精析例1：根据下列条件，求a:b的值：（1）4a=5b；（2）.78ab（2） ，∴8a=7b，∴7.8ab78ab解：（1） 4a=5b，∴5;4ab例2：已知，求的值.解：解法1：由比例的基本性质，得2（a+3b）=7×2b.∴a=4b，∴=4.解法2：由，得.∴,2723bbababa2723bba73bba733babbba4.ab23babbabaa，那么、各等于多少？2．已知cbba1．已知：线段a、b、c满足关系式且b＝4，那么ac＝______．，练一练1635122aaba,.bbb解：211333babba,,.aaaab,还有什么其他性质吗？dcba在等式两边同时加上1,得在等式两边同时加上1,得由此可得到比例的合比性质：如果，那么dcbaddcbbaddcbba问题2：已知a,b,c,d,e,f六个数，如果（b+d+f≠0）,那么成立吗？为什么？fedcbabafdbeca设,则a=kb,c=kd,e=kf.所以kfedcba.acekbkdkfakbdfbdfb☆等比性质....(...0)acmbdnbdn如果，由此可得到比例的又一性质：.......acmabdnb那么例3：在△ABC与△DEF中，已知，且△ABC的周长为18cm,求△DEF得周长.43FDCAEFBCDEAB解： ∴∴4(AB+BC+CA)=3(DE+EF+FD).即AB+BC+CA=(DE+EF+FD)，又△ABC的周长为18cm，即AB+BC+CA=18cm.∴△DEF的周长为24...