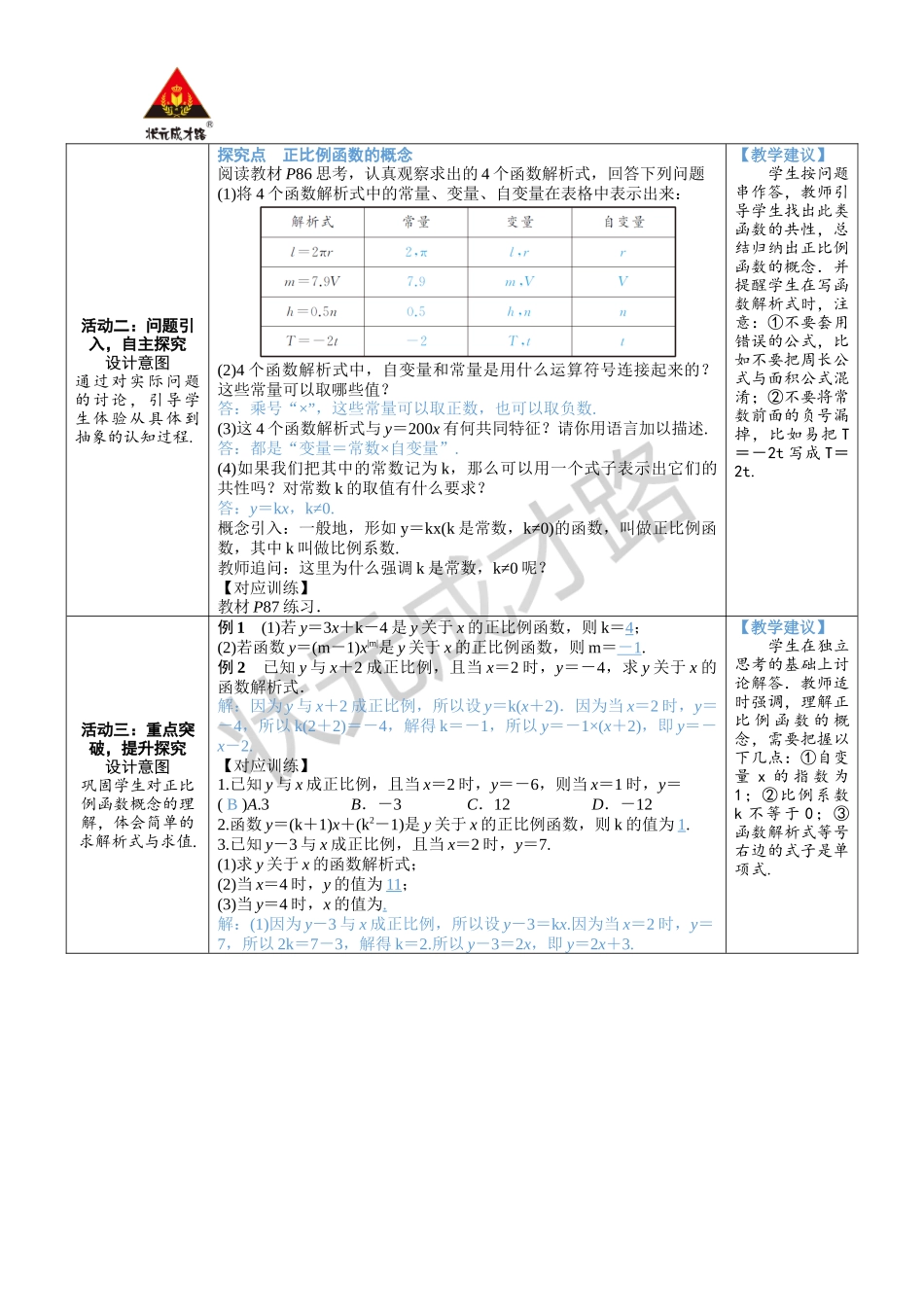
19.2一次函数19.2.1正比例函数第1课时正比例函数的概念教学设计课题正比例函数的概念授课人素养目标1.通过对不同背景下函数解析式的比较,理解正比例函数的概念,体会到正比例函数是反映现实世界的一种数学模型.2.理解并掌握正比例函数解析式,能根据已知条件确定正比例函数的解析式.3.能利用正比例函数知识解决相关实际问题.教学重点正比例函数概念的理解及其解析式的求法.教学难点正比例函数的概念的抽象概括过程.教学活动教学步骤师生活动活动一:设置情境,导入新课设计意图通过生活中比较生动的实例引入新课内容,激发学生学习的兴趣.【知识回顾】在小学时,我们曾经学过正比例关系,即两个相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为=k,我们不妨写成y=kx.【情境导入】(教材P86问题1)2011年开始运营的京沪高速铁路全长1318km.设列车的平均速度为300km/h.考虑以下问题:(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?(2)京沪高铁列车的行程y(单位:km)和运行时间t(单位:h)之间有何数量关系?(3)京沪高铁列车从北京南站出发2.5h后,是否已经过了距始发站1100km的南京南站?解:(1)京沪高铁列车全程运行时间约需1318÷300≈4.4(h).(2)京沪高铁列车的行程y是运行时间t的函数,函数解析式为y=300t(0≤t≤4.4).(3)京沪高铁列车从北京南站出发2.5h的行程,是当t=2.5时函数y=300t的值,即y=300×2.5=750(km).这时列车尚未到达距始发站1100km的南京南站.这个问题中得到的函数解析式有什么特点?函数值与对应的自变量的值的比有什么特点?带着这些问题,我们走进今天的课堂.【教学建议】教师带领学生回顾正比例关系的相关知识并引申至实例中的函数关系(正比例函数),比较实例中的函数关系与正比例关系的异同.教学步骤师生活动活动二:问题引入,自主探究设计意图通过对实际问题的讨论,引导学生体验从具体到抽象的认知过程.探究点正比例函数的概念阅读教材P86思考,认真观察求出的4个函数解析式,回答下列问题(1)将4个函数解析式中的常量、变量、自变量在表格中表示出来:(2)4个函数解析式中,自变量和常量是用什么运算符号连接起来的?这些常量可以取哪些值?答:乘号“×”,这...