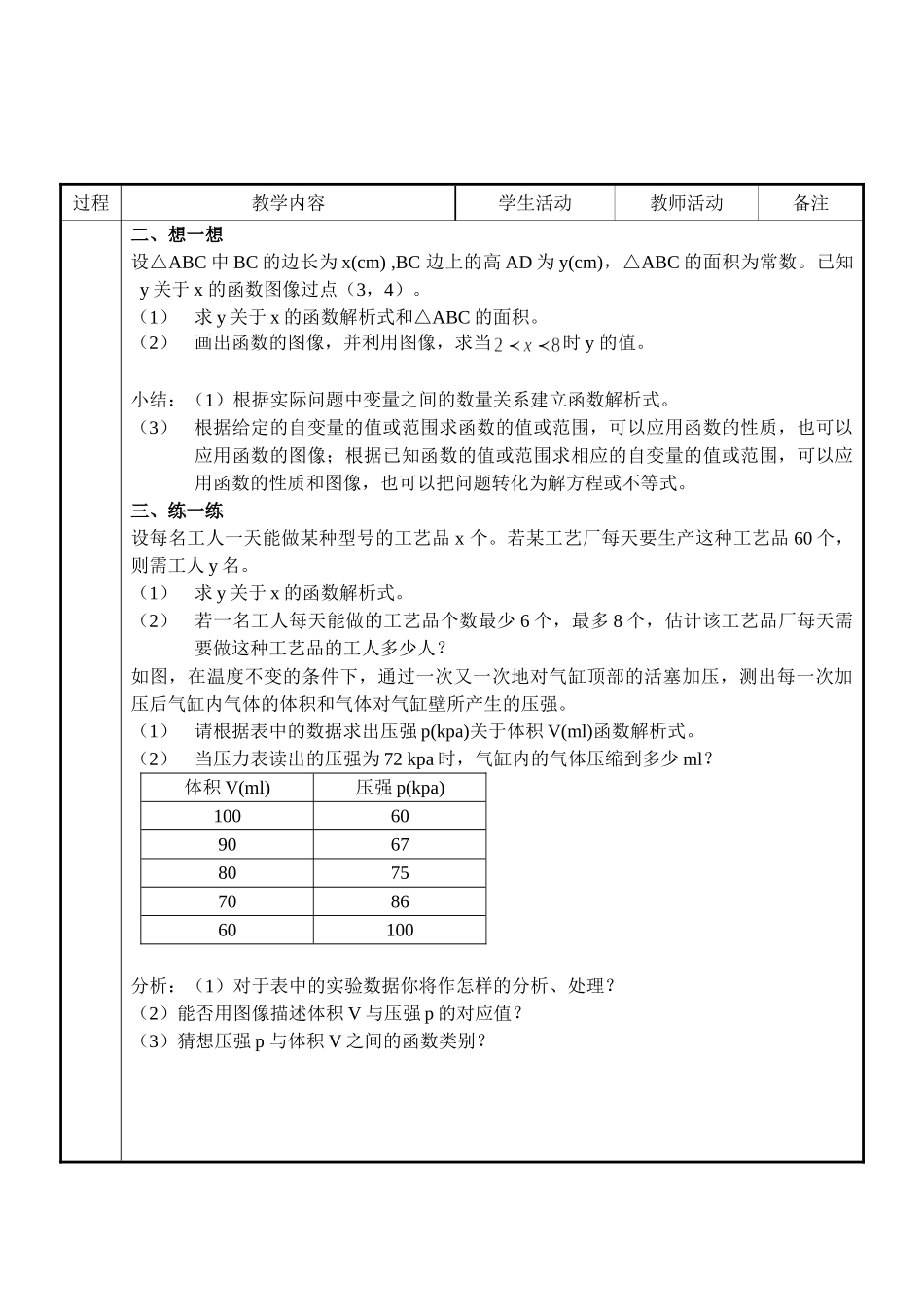
教师备课笔记上课日期月日星期教学课题6.3反比例函数的应用课型课堂形式纵横□/小组□/马蹄□/其它□人数教学目标知识与技能1、经历通过实验获得数据,然后根据数据建立反比例函数模型的一般过程,体会建模思想;2、会综合运用反比例函数的表达式,函数图象以及性质解决实际问题;3、体验数形结合思想。过程与方法让学生参与知识的发现和形成过程,强化数学的应用与建模意识,提高分析问题和解决问题的能力。情感态度与价值反比例函数的图像和性质在实际问题中的运用。教学难点:运用函数的性质和图像解综合题,要善于识别图形,勤于思考,获取有用的信息,灵活的运用数学思想方法。重点运用反比例函数的表达式和图象表示问题情境中成反比例的量之间的关系,进而利用反比例函数的图象及性质解决问题;难点例2中变量的反比例函数关系的确定建立在对实验数据进行有效的分析、整合的基础之上,过程较复杂,是本节教学的难点。板书设计教学辅助三角板ppt过程教学内容学生活动教师活动备注一、忆一忆1、什么是反比例函数?它的图像是什么?具有哪些性质?2、小明家离学校3600米,他骑自行车的速度是x(米/分)与时间y(分)之间的关系式是,若他每分钟骑450米,需分钟到达学校。序号过程教学内容学生活动教师活动备注二、想一想设△ABC中BC的边长为x(cm),BC边上的高AD为y(cm),△ABC的面积为常数。已知y关于x的函数图像过点(3,4)。(1)求y关于x的函数解析式和△ABC的面积。(2)画出函数的图像,并利用图像,求当时y的值。小结:(1)根据实际问题中变量之间的数量关系建立函数解析式。(3)根据给定的自变量的值或范围求函数的值或范围,可以应用函数的性质,也可以应用函数的图像;根据已知函数的值或范围求相应的自变量的值或范围,可以应用函数的性质和图像,也可以把问题转化为解方程或不等式。三、练一练设每名工人一天能做某种型号的工艺品x个。若某工艺厂每天要生产这种工艺品60个,则需工人y名。(1)求y关于x的函数解析式。(2)若一名工人每天能做的工艺品个数最少6个,最多8个,估计该工艺品厂每天需要做这种工艺品的工人多少人?如图,在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积和气体对气缸壁所产生的压强。(1)请根据表中的数据求出压强p(kpa)关于体积V(ml)函数解析式。(2)当压力表读出的压强为72kpa时,气缸内的气体压缩到多少ml?体积V(ml)压强p(kpa)1006090678075708660100...